計算の工夫とかけ算の順序

算数の教科書には、「計算の工夫」とか「暗算」という見出しで、結合法則等を使って計算を楽にする方法が載っている。結合法則などの法則と、100や1などの切りがいい数値を作る方法とが、組み合わされていることが多い。もちろん、計算の工夫としては、初歩的なものばかりなのだろうが。

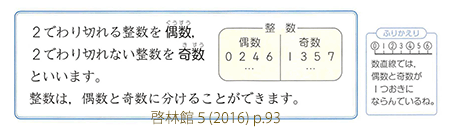
１）結合法則の利用
82+43から順番に計算するのではなく、足し算の結合法則を使って、43+57=100など、切りがよい数値を作る組合せを見つけて、それを先に計算する。

今度は、足し算ではなく、かけ算の結合法則と、25×4=100、125×8=1000などを併用する方法。12を4×3に分解して、結合法則により、25×4を作る。100ができると、計算が楽になり、暗算も可能になる。

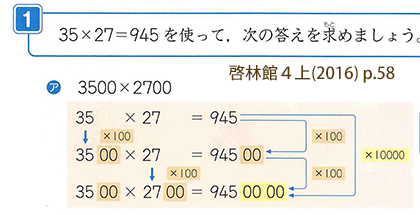
0が末尾に並ぶ数とのかけ算では、その数を10や100とのかけ算に分解して、それ以外の項を掛けてから、その結果に、10や100を掛ける（0や00を追加する）とよい。筆算でも使える方法である。これは結合法則を使っていると見なすことができる。

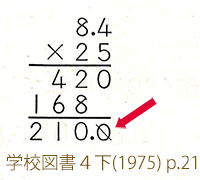
掛けられる数・掛ける数ともに、0や00で終わっている場合にも、この方法は使える。また、小数の掛け算の筆算は、1.92を192×0.01に分解して、整数部だけをまず計算し、後から0.01を掛けている（小数点を左にずらしている）と言える。「工夫」と言うほどのものではなく、当たり前にやっている。

２）分配法則の利用
分配法則と、35+65=100といった切りがよい数値を作る計算を併用する。7.2×の共通部分を括弧の外にくくり出して、35+65=100を作ることで、計算を簡単にする。実際の計算では、35+65のような幸運な組合せが発見できるとは限らないが、発見できればこの方法が使える、ということである。教科書の「計算の工夫」の節にあるような練習問題は、もちろん、その練習ができるように、数値が作為的に設定されているのだが。

105=100+5と分解して、100×6のような、計算が楽な部分式ができるように、分配法則を適用する。

99=100-1と言い換えて、100を作ることで、計算を楽にしている。＋の分配法則ではなく、－の分配法則の適用を含む。

分数の計算での、分配法則の利用。1/4+3/4=1という、切りがいい数値を作る数の組み合わせが併用されている。分配法則の使い方としては、共通部分を括弧の外に括り出すのが通例だが、(1/3+1/4)×12のように、括弧の中に分配したほうがよい例もある。

３）その他
割り算では、割られる数と割る数を同じ数で割っても（掛けても）答えは同じ、という性質の利用して、割り算を簡単にすることができる。

割られる数も割る数も、0や00で終わっているなら、10や100でともに割っておく。小数の割り算の筆算で10や100を掛けて小数点をずらすのも、同じ性質を使っている。「工夫」ほどのものではなく、筆算の手法の一部だと言える。

足される数から引いたのと同じ数だけ、足す数に足しても、答えは同じという性質を用いて、足し算を暗算で行う。引き算では、引かれる数と引く数から同じ数を引いても（足しても）答えは同じである。
94-48 =(94+2)-(38+2) =96-40 =56

大日本教科書の、「もっと算数玉手箱」という、チャレンジしたい人のためのページには、小学生のガウスが使ったとされる計算の工夫が紹介されている。

これは、交換法則と結合法則を利用している、とも言える
1+2+3+4 =(1+4)+(2+3) =5+5 =5×2 =10

数列の昇順と降順の対応項どうしを足して、その合計を２で割る、という方法も、その続きの部分に、紹介されている。


４）交換法則の利用
かけ算を巡るネット上の議論では、事柄を極度に一面化するデマゴーグたちの扇動もあって、日本の学校算数ではかけ算は可換でないと教えられていると誤解され、非難されている。だが実際には、計算問題では、意味があまり重要ではないので、交換法則は、必要に応じて適用すべきことが、教えられているのである。

上の画像は、筆算に際して、交換法則を使うことで、筆算の行数を減らすものである。計算の工夫とは言えないが、8×7の九九の答えを忘れてしまったときでも、被乗数と乗数の数を逆にした九九を覚えていれば問題なし、というのも、交換法則の活用である。

実は、意味が重要となる文章題でも、立式後の計算では、順序遵守は求められず、交換法則を自由に適用して構わないとされる。次の例は、文章題立式後の筆算で交換法則を適用して、行数を減らす方法。

上の画像における、問４と問６は無関係ではなく、問４は計算問題、問６は文章題だが、問４で用いた、筆算での交換法則の適用を、今度は文章題でやってみようというもの。
このことをあえて式に組み込んで書けば、

3×38 ←一つ分×いくつ分の公式に従って式を立てる【立式部】
=38×3 ←交換法則の適用【計算部】
=114 ←筆算の結果を書く【計算部】

となる。

みかんは１人３個ずつで、組の人数は38人なので、１つ分×いくつ分の公式に従い、3に38を掛ければ必要なみかんの総数を求められると認識する。そして、筆算では、交換法則を使う。１つ分×いくつ分、単価×数量、速さ×時間などの公式に従った立式と、交換法則の適用とは両立可能なのである。つまり、掛け算の順序は交換法則と両立可能である。

次の例は、文章題で、立式後の＝で言い換えて行く計算部分で、交換法則と25×4=100を併用している。

すど氏が2017年8月にツイートして、それに対する生天目（なばため）氏の反応が炎上騒ぎとなった問題も（注１）、同じように解いてみよう。これは、教科書の「計算の工夫」の節にうってつけの例題である。

「１本85円の鉛筆を144本と，１冊144円のノートを15冊買います。合計はいくらでしょう？」

まず、単価×数量の公式を２度繰り返して、立式する。このことで、児童が85円の85を単価として、144本の144を数量と捉え、単価に数量を掛ければ合計が求まるがゆえにかけ算を使った、ということが、教師は確認できる。

85円（単価）×144本（数量）＋144円（単価）×15冊（数量）

次に、鉛筆の本数とノートの値段の数値が同じで、85+15=100と切りがいい数字になる組み合わせになるところに注目して、交換法則を適用し、乗号の前に114が来る形にそろえる。さらに、分配法則を使って、144×をくくり出すことで、85+15をつくる。最後に、144にその合計の100をかける、つまり、144にゼロを２つ追加する。

85×144+144×15 ←単価×数量のことばの式に基づき立式
=144×85+144×15 ←交換法則
=144×(85+15) ←分配律
=144×100
=14400

答え 14400円

注

注１
「「１本85円の鉛筆を144本と，１冊144円のノートを15冊買います。合計はいくらでしょう」という数値設定の問題，かけ算の順序的にすごく面白そうじゃありません？」（すど氏 2017/08/02 20:31）
「例えば「あなたが小学校の先生だとして，この数値設定の特徴に気づき，暗算で144×100=14400円と計算できる子を育てたいですか，育てたくないですか」的な問いを初等科数学科教育法の授業で教員志望の大学生に投げてみたらどうかしら。」(20:42)

「これに関しては明確に答えられます。「NO」です。
理想は頭の中で最適化された計算を「確かめ算（検算）」として行い、表記上はそれぞれ別の掛け算から合算する方式を記入する。
そして「144×100のようなずるをした？」という問いに「いいえ」と答えられるようになるまでが「教育」です。」（生天目氏 2017/08/04 08:54）

すど氏の問題点は、彼が、算数を十分に研究しておらず、そのために、自分が作った設問が、計算の工夫という題で算数で教えられている設問の類題にすぎないということを認識できずに、あたかも、算数では計算の工夫が教えられていないかのように、そしてまた、それがかけ算の順序と相いれない例であるかのように提示しているところである。

「暗算で144×100=14400円と計算できる子を育てたいですか，育てたくないですか」と問うすど氏の問いに対して、生天目（なばため）氏は、「これに関しては明確に答えられます。「NO」です。」と答えているのであるが、「育てたいですか」にNOなのか、「育てたくないですか」にNOなのかが、不「明確」であり、生天目氏はまったく、明確に答えているとは言えない。たぶん、「育てたいですか」にNOと言いたいのだろうが。

生天目氏が理想とするのは、144×100で検算するが、式は単価×数量の公式に従って書ける児童の育成である。そのあと、「「144×100のようなずるをした？」という問いに「いいえ」と答えられるようになるまでが「教育」です。」と述べているのだが、この箇所が理解しにくい。

教師が「家に帰るまでが遠足です」と言ったなら、それは、学校で解散したら、もう教師の責任はないというのではなく、家に無事帰ったことを確認できて、はじめて教師の管理責任は完了する、ということであろう。それからすれば、生天目氏のこの部分は、児童が「ずるをした？」という教師の問いに「いいえ」と答えられるようになってはじめて教育は完成する、という意味になる。教育がそんなに簡単に完成してよいかどうか問題だが、ここは、買い物の合計を計算する文章題の指導が一応終わる、ということであろう。

だが、「いいえ」と答えられるようになる段階というのがどんなものなのか、ということが、生天目氏の文章からはよくわからない。「「いいえ」と答える」というのは、144×100で計算することが「ずる」でなく「検算」であることが理解できる理想的な段階のことなのか。それ以前の発展途上の児童たちは、計算の工夫を「ずる」だと捉えている、ということなのか。しかし、上で見たように、計算の工夫は算数で繰り返し教えられている。文章題でも、計算の工夫をしてよいのである。

生天目氏には、かなり特異な教育観があり、この反応は、そこから出てきたもののようだ。生天目氏にとって、学校は、わざと間違えてあげる、今初めて知った、今初めてわかったふりをしてあげる苦労を思い知る場なのである、と言う（2018/12/23 16:23）。

ともかく、生天目氏のこのツイートは炎上することになるのだが、その原因は、144×100で計算することを「ずる」ととらえるその発想そのものである。生天目氏は、「ずる」と言ったのは、自分自身ではなく、自分のツイート中の登場人物（教師）であると述べて、言い逃れを試みているが、その登場人物を創作して、登場人物にそのように言わせたのは、生天目氏自身である。

この炎上騒ぎに関連して、小学校の先生が交換法則の適用をズルと言ったという証言がなされた。

「25の48パーセントは48の25パーセントも答えは同じだから、48を4で割れば暗算できると言ったら、小学校の先生からそんなズルを先生が言ってはいけない、と非難された…」（数学氏 2018/11/05 11:47PM）

だが、ここでも、掛け算の順序や公式の適用と、交換法則の適用とは共存可能なので、交換法則の適用は「ずる」だという必要はない。まず、基準量×割合の言葉の式に従って、立式する。

25×0.48

立式したあとは、計算過程に入るので、どれが基準量でどれが割合がどれでということは、気にしないでよい。結合法則などを使って、計算を楽にすることもできる。

25×0.48
=25×(0.12×4)
=25×(4×0.12) ←交換法則
=(25×4)×0.12 ←結合法則
=100×0.12
=12

「48の25パーセントも答えは同じ」というは、式にすると少しややこしくなるが、次のように計算している、と考えることができる。

25×0.48
=0.48×25 ←交換法則
=(48×1/100)×25
=48×(1/100×25) ←結合法則
=48×25/100
=48×1/4
=12

計算の工夫は「ずる」でも何でもない。そして、どれが単価でどれが数量であるかという意味と関係を捉えた上で立式できることも、交換法則や分配法則などを使って計算の工夫ができるようになることも、どちらも、算数では目指されている。

（2019/01/01 21:11などのツイートに基づく）

小数の筆算でゼロを消すことの意味

「姪っ子の小3算数テストの採点結果。.0の有効数字に意味があるというのに全く訳がわからない。」（kennel氏 2016/11/16 04:33）

2016年11月から翌年にかけて、3.9+5.1=9.0という小数の筆算で、9.0のゼロを斜線で消していないために減点するテストの採点が、ツイッターやブログなどで、激しい非難を浴びた。日本の算数教育がおかしくなっているのではないか、というのである。茂木健一郎氏のように、これを子どもに対する虐待だとして非難する者まで現れた（注１）。その発端が、上記のkennel氏のツイートである。

この答案は、さらに、テレビの「林先生が驚く初耳学」というテレビ番組（2016年12月25放送）でも、取り上げられた。算数教育がどうあるべきかという議論を、権威で解決しようとする林修氏のやり方が正しいかどうか、ということは、ここで措いておくことにしよう。林氏は、京都大のフィールズ賞受賞者でもある数学者の森重文氏を訪ね、こうした採点の仕方の妥当性をきいた。森氏の回答は、最初に「できるだけ簡潔な表現にせよ」という指示がないのであれば、自分の感覚では、減点はない、9.0で何が悪いのか、というものであった。

森氏が「できるだけ簡潔な表現にせよ」という指示がないならば」と条件を付つけて言っていることに注意すべきである。たしかに、kennel氏のアップした答案の問題文には、そのような指示か書かれていない。だが、できるだけ簡潔な表現にするのは、算数・数学では、それが問題文にいちいち書かれていないなくても、しばしば求められることである。「数字は10進法で書く」というのと同様に、あまりに自明なことなので、問題文にはいちいち書かれないのである。それは算数・数学における「書かれざる指示」の１つなのである。

だから、3+5×(9-3)のような計算問題で、=3+30で式を終わらせたら、バツにされてしまう。 =33まで書かなければならない。

3+5×(9-3) =3+5×6 =3+30 =33

3+5×(9-3)と3+30と33の３者は等しいのであるから、3+30でも答えは間違っていない、とは主張できない。その理屈がもし通るなら、
3+5×(9-3) = (9-3)×5+3
と書いても、たしかに等号は成り立っているので、正解だということになろう。3+30のままで終わらせたら、未だ計算が終わっていないと見なされるであろう。計算問題では、しばしば、単一の数値になるまで、式を短くすることが求められている。


分数の計算問題や分数の計算が必要な文章題では、式の最後に出てくる分数は、もうこれ以上約分できない既約分数にしておかなければならない。このことは実は教科書には書かれているが、計算問題の一問一問に、指示が書かれているわけではない。既約分数になっていないと、そのような指示に従えていない、または、約分できるのにそれに気づいていない、としてバツにされ、やり直しとなる。「できるだけ簡潔な表現にせよ」という指示は、実際には、存在するのである。

Ａ）有効数字
kennel氏のツイートに戻ろう。kennel氏は、自分の姪の答案について、「.0の有効数字に意味があるというのに」と述べているが、これは２つの点で、間違っている。

第１に、有効数字は、中１で初めて学ぶのであり、この小３ではまだ学んでいない。このテストは小３の単元テストである。小３が、習っていない有効数字の処理を求められているはずはない。小３の授業やテストでは、有効数字の知識をもっていることは、そもそも、前提されていない。有効数字を理由としてバツにされることも、マルにされることもない。

有効数字では、小数点以下の位の数や数値が、精度を表しており、勝手に除去してはならない。しかし、ここでは、有効数字の処理は求められていない。求められていなくとも、中学で習う有効数字を先取り的に学んで、それを使って解答したなら、それは褒めてやるべきではないか、と言う人もいるだろう。

だが、それは、ありそうもないことである。kennel氏の姪は、別に有効数字を知っていて、それを適用して、斜線を引かなかったわけではない。

「姪っ子には親である弟が有効数字について説明し、この話はこれで終わりにしています。姪っ子本人はケロッと気にしていないそうなので皆さんご心配なく。」（kennel氏 2016/11/19 23:08）

と書かれていることからすれば、あとから親から教わったのである。有効数字を理解した上でケロッとしているのか、理解できないままケロッとしているのかはわからない。減点で「虐待」（茂木健一郎氏）を受けているのではないことは、確かである。ただ、彼女は斜線を引き忘れただけなのだ。kennel氏は、有効数字の処理に馴染んでいる大人の視点を、よく考えずに、算数のテスト問題の採点に対する評価に持ち込んでしまっている。

ツイッターなどで、算数の採点答案が問題視されるとき、その問題視は、より上の学年に獲得される概念を無意識に持ちこんでしまったことで、多くは起きている。

たとえば、かけ算の順序問題も、算数ではかけ算は〈一つ分×いくつ分〉という非対称図式で導入されるということに十分に配慮せずに、中高での、〈因数×因数〉の対称的な掛け算の学習を通じて養われる、〈順序のどうでもよさ〉の感覚を、算数教育に関する議論に、持ちこんでしまうことで、起きている。

ゼロを含む倍数概念も、同様である。高校や大学では、倍数は、ある整数（負の数、ゼロ、正の整数）について、その整数倍となる数である。倍数には、ゼロ倍のゼロや、〈負の整数〉倍も含まれる。そしてまた、〈負の整数〉やゼロについても、倍数を考える。だが、算数では、倍数にゼロは含まない。倍数は〈正の整数〉の〈正の整数〉倍なのである。たとえば、３の倍数は、１倍である３から始まり、２倍の６，３倍の９……と続く。

高校数学　３の倍数：... -6, -3, 0, 3, 6, 9, 12 ...
算数　　　３の倍数：3, 6, 9, 12, 15, 18 ...

算数では負の数を扱わないので、高校と同じ定義にすることは、もとより不可能である。それに、これはだいたい、定義なので、どちらが正しいというものではない。たしかに倍数のような基本的な概念は自己流に定義して使うのはまずいが、人々と意思疎通が可能な標準的な定義に従うべきであろう。そして、算数の倍数定義は、歴史的に見ても、常識的な定義である（注２）。高等数学で学ぶ倍数定義を、唯一正しい倍数の定義だとして無意識に考えてしまうために、それを外れている算数の倍数概念が不合理で非常識だと感じられるのである。

kennel氏のコメントも、既述のように、まさに、中学で習う有効数字の知識を、小学校の算数のテストの採点答案に対する評価のなかに持ちこんでしまっている。


第２の問題点は、有効数字の考えは、数学で扱われる数値には適用できないことである。算数・数学で使う多くの数値は、測定値ではなく厳密値なので、そもそも、かりに有効数字が既習であっても、適用できないのである。算数や数学で4.1cmとあったら、ぴったり4.1cmでおよそ4.1cmなのではない。算数や数学のテキストに現れる多くの数値は、誤差を含んでいない。


Ｂ）ゼロを消す

小学校の単元テストは、授業でやったこと、学んだことができるかどうかの確認のためのものである。授業で、小数点第１位までの小数どうしの足し算・引き算の筆算の際に、小数点以下のゼロを、斜線で消すことを習ったなら、ドリルやテストでも、それができるかどうかが試されるのである。そのゼロを消し忘れているから、減点されただけだと言える。

だが、どうして、算数では、小数点以下にゼロしかないときに、そのゼロを斜線で消すというような指導の仕方をするのであろうか。小学校の教師は、理由も必然性もなしに、そんなことを児童にさせているのであろうか。勝手なルールを作って、素直な小学生に従わせ、人を思い通りに動かす「独裁者」の感覚を楽しんでいるのであろうか。

そういうわけではない。小数点以下にゼロしかない数値のそのようなゼロを斜線を引いて消すのは、まず、１）そのゼロが不要だからであり、次に、２）既習の整数に関係づけるためである。ちなみに、その斜線が右上から左下にではなく、左上から右下に下ろす斜線であるのは、１などと取り違えないようにである。

１）有効数字が問題となりえない以上、小数点以下にゼロしかない数値のゼロは、省略可能である。もちろん、在ってももいいが、付けるだけ無駄なのである。9と9.0は数量的にはまったく等しいので、同じく等しいのなら、表現はできるだけ簡潔なほうがよい。だから、むしろ、消すべきである。数学で扱う数値は測定値ではなく、誤差をまったく含まない厳格値なので、小数点以下の桁数を気にする必要はない。

数値のなかに使われる数字のゼロには、省略が不可能なゼロとそうでないゼロとがある。省略できないゼロとは、たとえば、2005や9.03のなかのゼロである。これに対して、007や9.0、9.00000のゼロは、省略可能である。斜線を引いて消させているのは、児童がそうすることで、省略可能なゼロとそうでないゼロの区別を学ぶためである。

２）２つ目の理由は、既習の整数と関係づけるためである。kennel氏の答案は３年生の単元テストからのものである。小学生は３年生ではじめて小数を習う。小数を学び始めてから数週間後には、小数の足し算・引き算を習うのである。

その小数の導入の仕方であるが、それは「はした」という概念を使って行われる。「はした」というのは、「はんぱ」ということである。実際にある事物の、長さにしても重さにしても、単位となる基本的な量と等しかったりその倍数になったりすることは、稀である。ちょうど1m、ちょうど2mとは限らず、はんぱな長さや重さのものも多い。そのはんぱな長さや重さを数で表すには、どうしたらよいであろうか。そこで必要とされたのが、分数と小数である。

簡単な分数は既習なので、まず、１の1/10となる量を考えて、それを0.1と小数で表すこととする。教科書では、このようにして、小数が導入される。そして、それがいくつ分あるかということで、半端な量を表そうというのである。たとえば、１Ｌと少しの水は、リットルという大きな単位ではうまく表せない。その少しはみ出た部分を、１Ｌの1/10である、0.1Lを考えて、それが２つ分に相当するのなら、1.2Lとするのである。

整数は、英語では、whole numberと呼ばれる。つまり、整数とは、完全な数なのである。ということは、小数や分数は不完全な数ということになる。少なくとも、歴史的には、整数に対して、小数や分数は不完全な数を表すための苦肉の策として考案された、ということが、言語的な表現から推測される。小数や分数は特殊な数なのである。

だが、小数や分数が整数に対して劣った、不自然で、不完全な数だとかいった感覚は、大人にはない。むしろ、逆に、有理数も実数も知っている大人にとって、整数こそが小数や分数の一種で、ただし、それはたまたま、小数点以下にゼロがずっと並ぶ、特別な小数なのである。分数だったら、分母がたまたま１である特別な場合なのである。整数は、切りがいい、とても稀で幸運な小数のことなのである。

しかし、整数しか知らず、小数を学び始めた小学生の感覚には、分数や小数は、不完全な数だという理解のほうがフィットするでのであろう。というのも、小３は、それまで学んできた整数に加えて、半端な量を表す小数を学び始めたところだからである。小数が導入された直後の小学生（小３）の認識では、はんぱが出る特別な場合だけ、小数が登場するべきなのだ。小学生の認識では、9.0は「はんぱ」がないので、小数表現のような苦肉の策を取る必要がなく、従来通り、9という完全な数として表現すればよいのである。その意味でも、9.0の0を消されるべきものである。こうして、9.0が既習の9と関係づけられる。

次の画像は、1985年の、３年ではなく４年の教科書からのものである。この時代には、小数の足し算・引き算の筆算は４年ではじめて学ぶものであった。0.70が0.7と等しいこと（7.0が7と等しいことではなく）に対する子どもの認識を表す挿絵である。大人にとっては、0.70が0.7と等しいことはわかりきったことである。

3.9+5.1の筆算では、まず、小数第１位について。0.9と0.1を足す。これは、一方に0.1が9つ、他方には0.1が１つあり、両者を合わせれば、の0.1が10こになる。0.1は1を10等分した量なので、それを10個集めれば、元の1に戻るはずである。元の「完全な」数に戻ったのである。不完全な数字に必要だった小数点がある数字が、完全になることで、不要になったので、消す必要があるのである。だから、ゼロを消して、整数にしたのである。

小数の筆算で、計算結果の数値が小数点以下にゼロしかない場合にゼロを斜線で消させるのは、このように、１）既習の整数である9と同じものであることを確認するため、である。整数は習っているが小数をこれから初めて学ぶという段階で、小数が既知の整数とどう関わるのかが問題になるのは、自然なことである。筆算の結果でてきた9.0は、これまで親しんできた、1, 2, 3,... 9の9と同じことなのだ、ということを学ぶためにこそ、斜線を引かせるのである。３年で0.1は、１の1/10として導入される。だから、0.1が10個集まると、馴染みの1に戻るのである。

ツイッターで、今の小学校では9.0≠9と教えられているのか、と反応した人がいた。小学校で小数がどのように学ばれているかを知らない者には、たしかに、kennen氏がアップしたあの答案画像は、そのように見えるかもしれない。9.0は9と等しいので=9.0でもよいのに、減点されたということは、日本の算数教育では、9.0と9は等しくないと考えられているから、というわけである。実際には、その減点は、小数点以下のゼロを消すという指示を守れていないからつけられた教育的な減点である。学校のテストの減点やバツには、このような教育的な減点・バツが珍しくないが、それが数学的・計算的な減点・バツと誤認されることで、こうした誤解が起こるのである。

実際には逆で、9.0は既習の9と等しいこと、つまり9.0=9、であることを、わかるようにするために、小数点以下の要らないゼロを斜線で消させているのである。9.0と9が違うものだと思っている児童は、斜線でゼロを抹消することはできない。数学的には9.0=9であることがわかっている大人には、このように斜線を引いて消す訓練は、もちろん、不要である。測定値でないのなら、好みや必要に応じて、9.0のままにしてもよいし、9と書いてもよい。

9.0が9と等しいことを学ぶために、ゼロを線を引いて消している、というこの教育的文脈は、答案がネットにアップされてしまうと、脱落してしまう。そして、教育的文脈を知らない大人たちによる誤解に晒されるのである。そして、最近の日本の算数教育はなんてひどいのだ、ということになってしまう。自分自身も、小学生の頃に小数点以下のゼロを斜線で消していたことをすっかり忘れて、そう思うのである（注３）。

Ｃ）ゼロを追加する

逆に、ゼロを追加したほうがいい場合もある。小数の足し算筆算の習い始めでは、小数を習い始めたばかりの小学生は、9+2.6という計算問題で、9と6を同じ列に書いてしまうことで、=3.5と、間違った答えを書いてしまいがちである。小数の足し算・引き算で、注意しなければならないのは、このように位をそろえることである。このときは、むしろ、逆に、9は9.0に直したほうが、こうしたミスを避けられる。もちろん、慣れてくれば、不要になることであろうが。

3.6+0.835 = 3.600+0.835 =4.435
3.6のあとに、要らないゼロを追加するのは、これは、0.855と桁を合わせるためである。追加することで、3.600+0.835という小数の足し算は、3600+835という既習の整数の足し算の筆算と同じようにできる、ということが、より容易に見てとれるようになるのである。整数として足し算の筆算を行い、小数点の処理は後からすればよい、というわけである。桁がそろっていない小数どうしの足し算・引き算は、既習の整数の足し算を土台にして行われる。

0.001のいくつ分という説明の仕方を使って言えば、3.600は0.001が3600個分、3.600は、0.001が835個分なので、2600+835という足し算の筆算でまず、4435を求める。しかし、これは本当は、4435なのではなく、0.1が4435個という意味なので、本当の答えは4.435になるのである。整数の筆算と同じようにできることを理解してもらうために、ゼロを追加するのである。

注

注１
茂木健一郎「小学校の算数にまかり通っている「奇習」は、子どもたちに対する「虐待」である」(2016/11/20)
http://lineblog.me/mogikenichiro/archives/8305779.html
「昨日、小学校の算数のテストで、「3.9+5.1=9.0」と書いたら、減点されたというツイートが流れてきて、とてもびっくりした。これははっきり言って一種の子どもに対する「虐待」である。」
「小学校の算数で、そのような奇習がまかり通っていることは国の恥と言うべきことだろう。」
「奇妙な「正解」を押し付けるのは、子どもの精神に対する虐待であり、許されることではない。」

注２
本ブログの別記事「倍数はゼロを含む？ 」(2019/05/02)を参照のこと。
http://flute23432.blogspot.com/2019/05/blog-post.html

注３
茂木氏はまた、上記（注１）に引用した文章において、「ふしぎに思うのは、ぼくが小学生の頃は、「小数点」「かけ算の順序」「たし算の順序」といった問題は経験した記憶がないということで、いつからそんな奇習が小学算数の一部に広がってしまったのだろう。」とも述べている。

彼が実際にどのように教わったかは、茂木氏が実際に小学校で受けた授業がどんなものだったかを再現できる資料がないとわからないが、かけ算の順序は、戦前から続くかけ算指導法であり、小数の筆算で不要なゼロを抹消線で消すのも、遅くとも1970年代から続いている教え方である。茂木氏が記憶が無いというのは、教わっていないから記憶が無いのではなく、そう習ったのに忘れているだけであろう。

これらは、斜線でゼロを引く教え方が昔からあることを示す証拠である。画像上は、①1971年、中は②1975年の４年の算数教科書から。茂木氏はこの時代に小学生だった。下は、③1929年の教科指南書から。①では、斜線ではなく横線になっている。③には斜線はないが、5.00のゼロは消すのが普通であることを教えておく必要がある、としている。啓林館の1973年の教科書も、同様に筆算ではゼロに斜線は引かないが、6.00は6とする、と書いてある(p.109)。小数の筆算で不要なゼロを抹消させる教え方は、最近の現象ではない。

抹消線でゼロを消すルールは、整数や小数の四則演算を学習中の児童のために、小数の筆算の導入時に教育的な意味で一時的に設定されるもので、中学生以上には求められない。それは学年が進めば乗り越えられ不要になるものだから、忘れるのは当然であり、忘れていること自体は、健全であると言える。
忘れているかもしれないということに対する自覚がまったくなくて、高等数学を学んだ自分の感覚を、子ども自体の頭のなかに投影して、虐待だと言うのは、しかし、不健全というほかはない。



（※ すずすけ氏ブログ記事「小数の和と差の末尾のゼロに斜線を引かせる指導の根拠について調べてみた」（「パパ教員の戯れ言日記」2017/01/06）に対するコメント(2019/04/15)に基づく。）

倍数はゼロを含む？

日本の算数では、倍数には、ゼロ倍のゼロを含めていないで定義されている。「整数をかけてできる」と書かれているが、算数では整数とは、ゼロと正の整数のことで、負の数を含まないが、ゼロを含んでいる。３でも４でも、ゼロ倍すればゼロになるはずだが、ゼロ倍は除外されている。また、ゼロについても、その倍数を考えることはない。

「０は、倍数には入れないことにします」という、ゼロを除外する但し書きが入っている点で、定義としてはすっきりしないが、しかし、これは、「正の整数（自然数）を掛けてできる数」と定義すれば、但し書きは必要がなかったのである。ところが、算数では、負の数を扱わないために、「正の整数」という言い方もできない。また、自然数という概念は中学になってはじめて学ぶ。

これに対して、偶数はゼロを含んでいる。

黒木氏は、ツイッターで、算数に見られるこうした定義を非常識で不合理であると言い、さらに、どのようにしてそのような「不合理」がまかり通っているのかが理解できないために、算数教育の権威たちが、闇の勢力として、教師たちをそそのかして、子どもたちにそのように教えさせているのだと、ネットにありがちな陰謀論を唱えている。

「保護者の人達は子供に「0は偶数？」とか「0は2の倍数？」と聞いてみて下さい。……「0は偶数」「0は2の倍数」と答えることができなかったらチョー算数に害されている。」（2017/08/08 10:39）

「 算数の教科書では本当に、倍数から0を除くという非常識で不合理なことをやっている」（Twitter 黒木氏 2019/03/20 06:59）

「現実のこの日本において「0は偶数だが、2の倍数ではない」と教わっている子供達が存在するという事実は驚きではないだろうか？これが現実の算数教育の姿。この件は氷山の一角に過ぎません。」（Twitter 黒木氏 2015/07/17 19:32）

「0がすべての整数の倍数であることを当然と思えないような低学力の人物が小学生に算数を教える仕事をするのは問題があると思う。そういう塾講師がいる塾については保護者のあいだでの情報交換で悪評が広まると思う。」（Twitter 黒木氏 2017/01/26 23:37）

「山本良和氏のような人達が教師に「偶数と2の倍数は違う」と子供達に教え込むことをすすめていたりするのです。教科書の内容もひどいし。日本の算数教育はチョー算数に支配されているのです。」（Twitter 黒木氏 2017/08/08 10:42）

黒木氏のツイートを読んでいると、あたかも、日本の初等数学教育においてだけ、おかしな倍数概念が教えられているかのように錯覚してしまう。しかし、外国の初等数学教育でも、倍数(multiples)は、ゼロを含まないものとして教えられているのは、珍しくないのである。

次の画像は、ドイツ語圏で使われている算数教科書 Einfach besser in Mathematik (2008)からのもの。7の倍数(Vielfaches)は7からから始まっている。

次は、Saxon Mathから。これは、米国で用いられている自習用算数のテキストである。３の最初の６つの倍数が列挙されているが、その倍数のリストはゼロではなく３から始まっている。

３つ目は、ニューヨーク州のコモンコア算数教科書Eureka Mathから。

４つ目は、Math Challengeという本から。

今度は、ネットで見つかるさまざまな数学学習サイト等を見てみよう。学習サイトには、小学生を対象としたもの以外にも、教師や一般の数学ファンを含めて対象としたものもあり、前者は、倍数にゼロを含めていないようだ。。

まず、Splash Mathでは、ゼロは含まれていない。

次は、math comから。ここでは、ゼロを含めているが、負の数は含めていない。最小公倍数は、最小の公倍数（ただし、ゼロを含めない）とされている。ゼロを含めれば、倍数の定義に但し書きは不要になるかもしれないが、最小公倍数の定義で、但し書きが必要になってしまう。

ゼロを含めていないのは、サイトの想定読者（対象）を小学生に限定していないからであろう。"Math.com is dedicated to providing revolutionary ways for students, parents, teachers, and everyone to learn math."

最小公倍数は、最小の公倍数（ただし、ゼロを含めない）とされている。ゼロを含めれば、倍数の定義に但し書きは不要になるかもしれないが、最小公倍数の定義で、但し書き(not zero)が必要になってしまう。

３つ目は、Tutorvista com。ここでは含めていない。

４つ目は、mathgoodiesというサイト。ここは含めていない。

５つ目は、Khan Academy。ここは含めていない。

６つ目は、Math Funである。ここは、ゼロを含めているページとそうでないページがある。これは、たぶん、幼稚園児から高校生までを対象としているためだと思われる。"The site aims to cover the full Kindergarten to Year 12 curriculum. "(about, mathisfun)

まずは、含めているページから。注に、負の因数や倍数もある、と書かれている。
"There are negative factors and multiples as well."

次は、含めていないページ。

７つ目は、BBC Schoolである。ここは含めていない。

８つ目は、Smartick Methodというサイト。ここは含めていない。

９つの目は、Illustrative Mathematicsというサイト。ここは含めていない。

外国でも倍数はゼロを含めずに定義されているからと言って、そのような定義が間違っていることには変わりない、ひどい定義が外国にもあることを示しているだけと、黒木氏は言うかもしれない。だが、少なくとも、「日本の算数教育の権威たちの仕業だ」という陰謀論は、嘘であることがわかるであろう。それとも、日本のその「闇の勢力」とやらは、海外にまでその勢力を伸ばしているとでも言うのであろうか。

そもそも、ゼロを含めない倍数の定義は、間違っているわけではない。ゼロを含める新しい定義を自明視・絶対視してしまうために、それが不合理で非常識で低学力に見えるのである。その凝り固まった高等数学的な先入見を放棄すれば、その非常識・非合理の外観は消滅し、自然と問題は解決する。

素数とか倍数・約数だとかいった概念は数論に属しているが、数論はゼロや負の数を知らなかった古代ギリシア数学で発達したせいで、それらの概念は、正の整数の範囲で考えれていることが多い。素数についてはゼロや１や負の数は考えないし、倍数も、とくに何の断りもなしに、正の整数の範囲で考えられていることが多い。

偶数・奇数も、倍数と同じ数論的な概念であるが、上記に見たように、算数では偶数にゼロが含まれる。これは、偶数と奇数は、整数全体を２つのグループに分ける、という役割を与えられていることが算数では重視されるせいであろう。ゼロをどちらかに分類しないと、偶数でも奇数でもない整数が存在することになってしまう。

中学では負の数を習うが、倍数がどうなるかについては、とくに何も言われていないようである。高校の教科書では、最近は、倍数にゼロや負の数も含めるようになってきている。これは、新しい定義である。

数研出版『数学Ａ』（2019年）には、次のように書かれている。

「２つの整数a,bについて、ある整数kを用いて、a=bkと表されるとき、bはaの約数、bはaの倍数であるという。……２の倍数を偶数…という」(p.118)。

東京書籍も同様の定義で、「-6も2の倍数… 0はすべての整数の倍数である」（数学Ａ 2015 p.58）と書かれている（注１）。大学の初等整数論でも、そのように定義されている。ゼロ除算を避けるためにb≠0という条件を付ける場合と、そうでない場合がある。つけない場合は、ゼロについても、倍数を考えることになる。ゼロの倍数はゼロ１つだけである。約数と一緒に定義しようとするとこの問題が生ずるので、ある整数（負の数、ゼロ、正の数）の整数（負の数、ゼロ、正の数）倍として、かけ算だけで倍数を定義してやればよい。

倍数のこの新しい定義では、偶数は２の倍数の別名にすぎない。偶数は倍数概念のうちに解消されるのである。
偶数　　　…－２，０，２，４，６…
２の倍数　…－２，０，２，４，６…

ただし、東京書籍の教科書に、次のようにも書かれていることは、興味深い。「この節では、とくに断りがない場合、約数には正の約数だけを考え、倍数は正の倍数だけを考えるものとする。」とある。ゼロや負の倍数は形式的には考えられても、使い様も使い出もないもの、ということなのだろう。

分数の足し算などでの通分や、長方形タイルで正方形で作る問題の解決、3日毎に来るアイス屋と4日毎に来るクレープ屋が次に、同じ日に来る日の予想など、倍数を利用して問題を解決できる実際的な状況を考えると、正の整数に限定した倍数概念は十分に実用的である。

自然数にゼロを含めない定義と、含める定義があるのと同様に、倍数にも、ゼロを含めない古い定義と、含める新しい定義がある。どちらが間違っているということはない。日本や外国の初等算数教育では、古い定義が採用されている。理科で小中学生がニュートン物理から学び始めるのと同様に、初等数学でも、より直観的で理解しやすい、絶対値の古い定義やユークリッド幾何など、古い時代の数学からまず学ぶのである。

ThinkMathという、数学教師向けサイトでは、ゼロを含めている（負の数は含めない）が、次のような注記があった。
http://thinkmath.edc.org/resource/multiple

「ある数の倍数を挙げるとき、子供は（そして大人も）その数そのものを挙げるのをしばしば忘れてしまう。そしてまた、ゼロを含めるべきかどうか確信が持てなくなることも、よく起きる。３の倍数は、３×０や３×１を含めた、３×整数、である。だから、３は３の倍数であり、５は５の倍数である。ゼロは、恐ろしく情報量がない倍数ということはあるとしても、すべての数の倍数である。しかし、ゼロはどんな数にとっても倍数であるので、それを列挙することはしばしば、役に立たない。そして、"最小"の倍数（たとえば、最小公倍数）が何かと問うとき、正の倍数しか含めていない。」

数論的な概念は、なぜか、ゼロ（倍数、偶数）や１（素数、約数）を含むのか、それ自身（約数）を含むのか、ということが、曖昧になりがちである。

注

注１
第一学習社や実教出版も同様の定義になっている（2019年、新版、高校数学、Standardなどがつかない版）。啓林館は、まず自然数の範囲で倍数・約数を定義して（数学Ａ2016 p.62）、少しあとで、整数全体に倍数・約数を拡張している（数学Ａ2016 p.71）。

補遺

補遺１
ユークリッドでは、倍数は「大きい数が小さい数によって割り切られるとき、大きな数は小さな数の倍数」（VII D5）と、定義されている。新しい定義でも、倍数は約数との関係で定義されている。だが、新しい定義との大きな違いは、負の数（－２，－４…）やゼロは、含まれないことである。

現代の日本の算数教科書とも違っているところがある。それは、２の倍数に２自身が含まれないことである。たしかに２は２で割り切れるが、ユークリッドが「大きな数が小さな数によって」と書いていることに注意すべきであろう。２と２は等しく、大小の関係にないので、２は２の倍数ではない。倍数は、その数より大きくなければならない。つまり、２の倍数は、その２倍の４から始まるのである。

１倍は倍のうちに入らない、ということになる。日常でも、１倍は同語反復の効果しかないから、１倍が倍として話題になることはないであろう。４や６なら、それより小さな２で割りきれるので、２の倍数である。同様にして、３の倍数は６から、４の倍数は８から、始まる。

一方、偶数・奇数は次のように定義されている。「偶数とは、二等分される数である。」(VII D6)。「奇数とは、二等分されない数、または、偶数と単位だけ異なる数である。」(VII D7) （池田訳）

２で割り切れるかどうか、等しく２つに分けられるかどうかで、偶数か奇数かが決まる。余りなしに分けられる数が偶数、１つ余ってしまう数が奇数である。奇数は「偶数と単位だけ異なる」とも言われる。「単位」と呼ばれるのは１のことである。奇数は偶数±単位（１）なのである。。

数とは「単位からなる多」なので、ユークリッドでは、１は数ではない、ということになる。１は等しく２つのグループに分けられないから、奇数ではないかと思いたくなるが、ユークリッドでは、そもそも数でないので、奇「数」でもない。

ゼロはどうかと言えば、西欧は長い間ゼロを知らなかったので、ユークリッドも、当然、知らなかった。だから、ゼロが偶数か奇数かは、ここでは、問題になりえない。ゼロの概念がアラビアから受容されても、当初は、ゼロは数ではなく、記号の扱いだった。数でないなら、偶「数」でもありえない。

ユークリッドでは、すでに書いたように、１は単位であり数ではないので、奇「数」でもない。２は数であり、二等分できるので、偶数である。３が最初の奇数である。
まとめると、ユークリッドでは

偶数　　　２，４，６，８……
２の倍数　４，６，８，１０……

であったのである。このように、ユークリッドでは、偶数と２の倍数は一致しない。偶数と倍数は別の概念なので、日本の算数で、偶数であるゼロが倍数には含まれないということに、どんな問題もない。


だいぶ時代が下って、1835年のノエルの『算術初歩』(J. N. Noël, Arithmétique élémentaire)では、どうなっているのか。

倍数については、「108 ある整数を他の整数回掛けてできた積を、倍数と呼ぶ。だから、４回掛けた5、つまり20は、5の倍数である。ある整数は、正確に複数回そこに含まれているとき、もう１つの整数の従倍数（約数 sous-multiple）である。」(p. 41)  ここで、整数と呼ばれているのは、正の整数であろう。

ある数の倍数に、その数自身（１倍）が含まれるかどうかは、例が挙げられていないので、この箇所の記述からはわからない。しかし、p.16に九九表があり、それを見ると、２倍（回 fois）から始まっていて、１の段がなく、つまり、１倍がないので、たぶん、最初の倍数は２倍の数だと考えられる。
ゼロはどうかと言うと、最小公倍数(le moindre multiple)について述べたところで(p.46)、とくにゼロを除くというような但し書きはないので、倍数にはそれ自身（１倍）だけでなく、ゼロも含まれない、と考えられる。

フランスのリセ算術教科書の古典とも言えるBriotの『算術書の基礎』（英訳 1865年）では、7は7の最初の倍数だと明白に言われているので、ある数の倍数は、その数そのものから、つまり、１倍から始まる。

（仏語原書  Éléments d'arithmétique, Paris, Dezobry, E.Magdeleine et Cie Libr. -Éditeurs, 1855.）

偶数についてはどうか。

「116 ２で割れる数は、常に、２つの完全（＝整数）で等しい部分に分けられ、この理由で、偶数(nombres pairs)と呼ばれる。… 対して、２で割れない数は、２つの完全で等しい部分に分けられないので、奇数(nombres impairs)と呼ばれる。１，３，５…などは奇数である。」(p.42)

偶数は２，４，６……、奇数は１，３，５…と、例が挙げられている。ユークリッドの時代と違い、１が奇数の例として挙げられていることから、１が数として認められたことがわかる。

偶数として挙げられたものには、ゼロは含まれていなかったが、しかし、そのすぐ後の箇所で、「０は偶数に数え入れられる」とある。ゼロについては、数(nombre)ではなく、記号(chiffre)という語が同時に使われていて、ゼロの扱いにまだ迷いが残っているようだ。

Briotの『算術書の基礎』では、偶数・奇数を説明した段落では、偶数にゼロは含まれてない。

以上のことから、19世紀初頭・中葉のフランス語圏では、偶数と２の倍数は次のようだった、と考えられる。
偶数　　　（０），２，４，６，８……
２の倍数　（２），４，６，８，１０……
ここでも、偶数と２の倍数は一致しない。

補遺２
偶数にゼロを含めるかどうかについては、現代でも、分かれるようである。日本の算数や、Shirley Tuckerの幼児向きの本、上記に例を挙げたSaxon Mathでは、偶数にゼロを含めるが、AAA Mathという数学学習サイトや、New York州のCommon CoreカリキュラムであるEureka Mathでは、含まれてない。このCommon Coreカリキュラムでは、日本の小学生が小５で習う偶数・奇数を小２で学ぶのだが、小２はまだ、ゼロを２で割る割り算を学んでいないせいもあろう。

補遺３
「小5の教科書で、0は偶数だが、0は倍数から除くと説明してあるのもひどい。数学の常識的には0はあらゆる数の倍数です。例えば4の倍数であることと下二桁が4の倍数であることは同値なのですが、0を倍数から除くと100で破綻します。子供の論理的読解力が算数教科書のせいで破壊されそう。」（Twitter 黒木氏 2018/05/13 08:05）

もし４の倍数にゼロを含めないと下２桁が00となったときに、４の倍数の判定法が破綻する、と黒木氏は言うが、下２桁が４の倍数か「または」ゼロのとき、と言えば済むことで、破綻は起きない。偶数にゼロを含めないBriotの『算術基礎』では、偶数は１の位がゼロか「または」、偶数の数字かで判定できるとしている。

（flute23432 2018/08/17 01:40などのツイートに基づく）
（2020/03/29 改定）