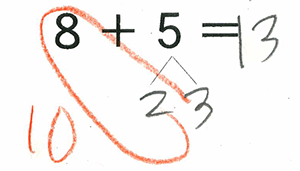かけ算の構造としての一つ分×いくつ分(被乗数×乗数)
文章題立式時のかけ算の式の順序
ゼロを含まない倍数概念
足し算での合併・増加
引き算での求残・求差
わり算での等分除・包含除
文章題の式欄・答欄
公式を使った説明や公式に従った立式
さくらんぼ計算
二重数直線図の使用
場面の翻訳としての式
など
〈かけ算の順序〉教育はその中核であるが、これは、彼らによると、超算数と彼らが呼ぶ問題群の全体から見ると、氷山の一角にすぎない。
さらに昂ずると、彼らの批判は「馬鹿」「クズ」という罵詈雑言が飛び交う非難とヘイトツイートに転化し、「小学校がトンデモ化している」、「数学ができない小学校教師が、算数教育の権威たちに植え込まれた嘘を、子どもたちに教えている」、「子どもたちを避難させないと危ない」といった、あらぬ方向に議論が暴走してしまう。ネットではこのようなことが起こりやすいが、すでにネットでのこうした議論を保護者が信じてしまい、学校と教師への信頼を失い、子どもが基本的な事柄を学び損ない、学年が進んで算数が分からなくなって不登校になる、などの弊害が起き始めている。
だが、騙されてはならない。こういった批判に根拠らしい根拠はない。彼らの批判は、多くは、高等数学で学ぶような概念や定義を、初等中等の数学教育にそのまま無思慮に持ちこむことで起きる誤解に発している。だが、初等中等の数学教育は、単に低レベルの数学なのではなく、同時に教育でもある。彼らにはこのことが理解できない。自分たちが知らない、算数教育固有の概念、古い数学の概念に出会うと、ただそれだけで、彼らはいかがわしいと思うらしいのである。
1) かけ算の説明に出てくる一つ分といくつ分だが、アレイ図を使えば(使わなくても、各皿のリンゴにa, b, c, d..と記号が書かれたラベルを貼れば)、一つ分はいくつ分と、いくつ分は一つ分といつでも解釈できるので、そのような概念や区別は無意味である。
― そのとらえ方を進めていくと、直積(Cartesian product)としてかけ算に行き着くが、直積は小学生には理解が難しい。これに対して、複数の同数グループ(equal groups)は、教室での配布物配布や班編成を例に使えるなど、小学生には一番分かり易いかけ算モデルである。同数グループタイプの文章題は正答率がとても高いが、直積タイプの文章題はとても低い。
各皿に4つずつとあれば、物理的近接性に基づいて1まとまりを4つとするのが自然な解釈で、トランプ配りやラベルを貼って、いくつ分を一つ分、いくつ分を一つ分とすることは、掛け順論争に参加してでもいない限り、大人でも思いつかない、かなりうがった解釈である。かけ算を学ぶ小2が自発的に思いつくものではない。
たしかに、教科書でも交換法則の説明に使われるアレイ図は、コマが縦横等間隔に並んでいるので、縦にも横にも列をとることができる。しかし、その場合でも、一つ分×いくつ分の枠組みは保持されるのである。つまり、縦の列でグループを作ると、それが横に4列あるので3×4,横に列を作ると、1列が4つで、列は3列あるので、4×3である。直積主義のように、グループを作らずに、縦と横の個数から直接、総数を求める、というところまでは行かない。
2) かけ算文章題の式を一定の順序(一つ分×いくつ分)で書くことを求め、もし逆順で書くとバツにして、掛け算の交換法則(可換性)を否定している。これは嘘を教えることで、悪い影響を残す。
― 1つ分といくつ分をそれぞれ押さえているかどうかチェックのために、書式として順序を固定しているだけで、この固定はかけ算の可換性を否定するものではない。
数量欄左、単価欄右の見積書を採用する会社で、新入社員が数量欄に単価を、単価欄に数量を入れたミスを上司が訂正させても、かけ算の可換性という数学的な原理を否定しているとか、かけ算は非可換であると社員に嘘を教えている、とは言えないが、それと同じである。
また、かけ算の順序に従って式を書くことは、基本的に、文章題の立式でのみ求められ、計算問題や、文章題の立式の語の計算(筆算など)は、求められない。
かけ算の可換性は、小学校では、繰り返し(小2,小3,小4で)教えられている。国際的なテストTIMSSで、加乗の可換性、減除の非可換性の理解を問う設問では、日本の中学生は比較上位で、かけ算の順序教育が、かけ算の可換性の理解を妨げる、とするのは、間違い。
3) 文章題では、与えられた数値だけを用いて立式することが求められ、文章中にない数値を用いると式がバツにされる。与えられた文章には25%とあるのに、式で÷4と書けば、バツになってしまう。むしろ、そのように言い換えられる児童のほうが、割合を理解できている。
― 小学生はまさに立式の仕方を学んでいるのであり、文章題からどのように、答えを求める式をどう立てたのかを、教師に診てもらう必要がある。そのためにも、文章題の数値を使って、文章題文章と式とのつながりを示すことが求められるのである。
ただ、これは原則であり、1ダース→鉛筆12本、テントウ虫の足→6本、5割→0.5などは、単位や生物、割合表現についての基本的知識から、計算に必要な数字を引き出す必要がある。
25%を÷4とするとバツになるのは、その文章題が、授業で習った、基にする量×割合=比べられる量の公式を使って答える設問であった、そしてまた、同時に、百分率を正しく小数に変換できるか、ということが問われていた可能性が高い。
4) 足し算には合併と増加があるとして両者をブロックの操作で区別させているが、同じ足し算であり、区別は無意味。区別するのは数学の抽象性を否定するもの。
― 足し算の意味は、足し算が適用できる体験可能な、具体的な状況や操作からはじめて理解される。数字や演算などの理解には、その生活世界的な意味基盤として、体験的な状況や行為への関係づけが不可欠である。このことの理解が、超算数批判論者には欠けている。
その状況や操作の基本的な類型が合併と増加である。合併は金魚がいない水槽に、左から2匹、右から3匹の金魚を同時に入れること、増加は、すでに2匹いる水槽に、金魚3匹を追加することである。
もちろん、小学生はこの2つの状況に、どちらも足し算が適用できることを学ぶ。もし、合併しか習わないなら、3年生になって、手持ちの530円に、今月のお小遣い800円もらったという、増加の状況で、足し算が使えるのかどうかがわからない。
引き算の求残と求差も同様である。ただし、合併と増加に比べて、求残と求差では意味の隔たりが大きく、求残で引き算を学び始めた児童は、どうして求差に引き算が適用できるのか、わからない。こういった困難はあるが、多くの児童はこの困難を乗り越えて、どちらの状況・操作タイプにも引き算が適用できることを理解するようになる。
5) 同じわり算なのに、等分除と包含除の2種のわり算があるかのように言っている。
― 超算数批判論者は、一つ分/いくつ分の区別を認めないので、一つ分を求めるわり算(等分除)といくつ分を求めるわり算(包含除)の区別も、理解できない。1)を参照のこと。
6) 算数教科書ではでは、倍数からゼロを除外しているが、これは「ゼロはすべての数の倍数」という常識に反する。
― 「ゼロはすべての数の倍数」は確かに高校で学ぶが、常識とは言えない。倍数や約数、自然数、素数など、ゼロや負の数を知らなかった古代ギリシアの数論の伝統に由来する諸概念には、多くの場合、ゼロや含める定義と、正の整数内で考えてゼロを含めない伝統的な定義があり、算数は含めない定義を採用している。定義が違うだけ。含めない定義でも、十分に実用的である。
7) 正方形を、特殊な長方形ではなく、長方形とは別の図形として教えている。
― 両者の包摂関係は、現代化算数の時代に教えられたが、多くの小学生がこれを理解できず、教育現場に大混乱を来した。だから、現在では、その関係はあえて教えられていない。
描かれた図形から長方形を選ぶ設問は、その名称の図形の(教科書に例示されているような)典型的な形を選ぶもので、包摂関係を前提としていない。したがって、包摂関係を否定してもいない。
算数では、正方形の面積の公式を、長方形の面積の公式とは別に学ぶが、これも、長方形の特殊な場合である正方形専用の公式を学んでいると見なせば、包摂関係を否定している、とは言えない。布は汎用のハサミでも切れるが、布バサミのほうが切りやすい、というのと同じ。
8) 繰り上がりがある1位数どうしの足し算は、さくらんぼ計算なくても答えは出せる。
― さくらんぼ計算を行った答案は、式の周辺に数字や線が書かれているので、確かに、大人には、異様に、そして複雑怪奇に見え、もっと簡単にできないものかと感じられるが、これは、大人が足し算九九をマスターしていて、すぐに答えが出せるからである。公文や珠算に通っている児童は、答えがすぐに出せるので、さくらんぼの描き方を覚える動機がない。
だが、さくらんぼ計算で、10のまとまりができると1つ上の位が1つ増える10進法の位取記数法の仕組みを理解することができる。足し算九九をマスターしている子も、今一度、原則に立ち戻る価値がある。
8+5 =8+(2+3) =(8+2)+3 =10+3 =13
9) 文章題の解答欄に式欄が答欄とは別に設けられ、教えられた方法に従う式でないとバツにされる。数学では、同じ問題にも解き方が複数ある。教えられた以外の解法を使った解答にバツをするのは、新しい解法を発見するという数学の醍醐味を否定するもの。
― 小学生はまさに、はじめて四則演算の立式の仕方を学んでいる最中で、同じ問題をさまざまな仕方で解決できる方法を提案したり発想したりする段階にはまだない。だから、教わった立式の仕方が習得できているかどうか、教師が診る必要があるので、式は答えとは独立に、採点・評価の対象となっている。文章題での式欄と答欄の用意は、フランス語圏やドイツ語圏でも見られる。それに、式を書くことで、答えが間違った理由が、単なる計算ミスなのか、それとも、割る数と割られる数を取り違えているためなのかがわかり、いわば診断結果を治療に生かすことができる。
単元テストのように、授業の一環として実施される確認・達成度テストでは、しばしば、教えた解法が習得できているかどうかをチェックするのが目的である。だから、教えたのとは別の方法で書いてバツになったり減点されたりする、ということが起きる。
だが、これは、けっして、他の解法が存在しない、ということではない。かけ算を学ぶ小2は、それが足し算でも電卓でもできることを知っているが、かけ算の文章題で、足し算の式を書けば、やはり、バツにされて、式の書き直しとなる。
10) 学校の算数は、割合や速さなどを公式を使って説明しており、公式暗記主義に陥っている。
― 教科書を見れば分かるように、なぜそのような公式になるのか(なぜ三角形の求積では2で割るのか、など)の理由・背景も、小学生は学んでいる。単なる公式暗記主義では公式は使いこなせない。このことを留意の上、学習事項のエッセンスを表す公式の暗記は肯定されるべき。
(東京書籍教科書5下, 2014, p.36より)
11) 割合や速さがくもわ図やみはじ図を用いて教えられている。くもわ図やみはじ図の使用は、思考せずに、機械的に正しい答えを出せる安直な方法である。
― これは事実誤認である。たしかに、使う小学校教師もいるようだが、メインにはなっていない。小学校の算数教科書や、ネットで見つかるPDFの指導案には、そのようなものは載っていない。メインは二重数直線図である。
それに、くもわ図やみはじ図で機械的に解決できる、割合や速さの文章題は、かなり単純なパターンのものに限られるのではないか。
12) 割合の問題に、児童は、理解を阻害する二重数直線図の描き方のようなつまらないこともまで学習し、それができるかどうかで評価される。
― 割合の文章題に含まれた、a:b=c:1という、2つの比とその対応関係を線の長さの割合などで視覚化する点で、二重数直線図はとても優れている。教師が二重数直線図を黒板に描くだけでなく、児童も書くように指導するのであれば、その描き方も学ぶことになる。確認テストでは、それが教えられたように描けるかどうかがチェックされる、ということは出てくる。もちろん、慣れてくれば描かなくて済むようになるが。
13) 21÷7の答えを求めるときに使う九九の段を尋ねる、単元テストの設問では、答えは割る数である7の段だというのだが、7×3を思い浮かべようが3×7を想起しようが、自由だ。
― 小3になるとわり算を習いはじめる。わり算の単元の最初のほうで、簡単なわり算の答えは、九九の割る数の段を使って(走査して)答えを見つける、と習う。21÷7は、7×1=7, 7×2=14, .. と、割る数7の段を走査して、答えが割られる数の21になったところで止まる(7×3=21)。その際の乗数3が答え。使った九九の段は、三の段である。
ドリルや単元テストには、次のわり算はどの段を使って答えを求めますか、という設問がある。この設問は、教科書・授業のこの教え方を前提とし、それを習得できているかどうかチェックするものである。
どの単独の九九を「想起」するのか、などとは尋ねていない。
14) 等号は両辺の式や数の大きさの等しさを表す記号なのに、算数では、計算結果を導く記号として用いている。
― 低学年生は、等号を、結果を導く記号と理解する傾向があるが、これは教え方に依存しないようで、外国でも見られ、そのような等号理解は、操作的(operational)と呼ばれる。両辺の同時的等量性の理解、つまり、関係的(relatinal)な理解は、大人が思うほど児童には簡単ではなく、一気にたどりつけるものではない。代数学を学びはじめる中学においてはじめて完成する。実際、等式の性質とそれを活用した方程式の学習は、中1で学ぶ事項である。
15) 式を、場面の翻訳するものと考えるのは、数式の抽象性を誤るものである。4×3と書いただけでは、4個ずつが3つなのか、3個ずつが4つなのかは、わからない。
― 文章題で式を立てることは、自然言語から数式を抽出することである。翻訳は、自然言語どうしで行うものなので、「翻訳」の比喩は、確かに、不適切である。
計算ができるのに文章題ができない児童は多い。文章題ができないということは、学んだ数学を生活や仕事に活用できない、ということである。そこで、算数では、文章題と式との対応関係が重視される。小学生は、文章題の文章から、どのように、複数の同数グループのような数的関係を引き出して、それに基づいて式を立てるのかを学ぶとともに、逆に、想像力を使って、式から文章題を作る、ということもやらされる。
文章題と式の対応を学んでているというこの状況では、初学者がつまずかないように、文章の表現を限定したり、式のヴァリエーションを制限したり、かけ算の順序を固定したりするなど、単純化やパターン化、制限などが必要となる。これが、抽象的な式が文章と1対1に対応すると見なされている、と誤解されやすい背景である。
16) 児童たちは、AIがなかった時代のロボットのように、思考せずに機械的なパターンマッチングで問題を解かされている。
― 授業参観を一度でもすれば、授業・学習が、整然粛々とした機械的な作業の連続ではなく、児童のトンデモ発言や、試行錯誤、混迷、気晴らし、うまく解決できた喜び、消しゴムの落下、などに満ちていることが分かる。
17) 3.9+5.1=9.0の筆算で、9.0のゼロを斜線を引いて抹消させるのは、有効数字を否定するもの
― 算数数学で使われる数値は、多くは、測定値ではなく厳密値であり、もともと有効数字が適用できるようなものではない。それに、小数の足し算の筆算は3年生で学ぶが、数値の精度を桁で表す有効数字の学習は中1になってからはじめて学ぶ。
(単元テスト 正進3年11.小数)
抹消していないとバツにされた採点答案は、小学校で9と9.0が等しくないと教えられていることを示しているように見える。だが、事態はむしろ逆で、小数9.0が既習の整数9と等しいことが分かる子だけが、.0を抹消できるのである。
ここには、単に小数の足し算の筆算だけでなく、小数点以下が0しかない小数は整数と見なせるという、小数と整数の関係の学習も、含まれていると考えるべき。分数の計算で、答えを既約分数にしなければならない、というのも、単に分数の計算だけでなく、約分の練習を含んでいるからである。
18) 超算数は、日本の算数教育の権威が、教師たちに布教しているトンデモ理論である。
― 「超算数」には、日本独自のもの(かけ算の順序)もあるが、ゼロなし倍数、合併・増加、図形の包摂関係の省略、みはじ図・くもわ図、一つ分/いくつ分、等分除/包含除、答えを導く等号、文章題との式欄/解答欄など、日本の専門家の権威が及ぶと考えにくい外国の数学教育でも、見られるのである。
次の2つの画像にうち、上は、みはじ図の英語版である。みはじ図と違い、形が円ではなく2等辺三角形になっている点は異なる。下の図は、アメリカの算数自習書SaxonMathからの引用である。偶数はゼロを含むが、倍数はゼロを含まない(ある数の倍数は、一倍であるその数そのものから始まる)。
(h3maths.edublogs.org, 2013/06/27)
(twitterに2018/10/17に投稿したツイートに基づく。)