それを見たネットユーザーたちは、日本の算数教育では、掛け算の可換性(交換法則)という数学的真理が否定されている、嘘がどうどうと教えられている、と学校や教師を批判する。このような炎上騒ぎが、毎年のようにネットで起きている。だが、掛け算の順序は、算数で教えられている交換法則とは、矛盾するように見えて、本当は、矛盾しないのである。
というのも、掛け算を「1つ分×いくつ分=全部の数」で考える限り、交換法則には2種類あって、算数で教えられている種類の交換法則は、かけ算の順序と矛盾しないからである。2種類の交換法則というのは、解釈的な交換法則と位置的な交換法則である。解釈的な可換性と位置的な可換性と呼んでももよい。
解釈的交換法則は、一つ分×いくつ分の順序を変えずに、×記号の前後の数値だけ交換するものである。これに対して、位置的な交換法則は、単に、一つ分といくつ分を書く位置を×記号の前後で交換したものである。だが、7と8の位置が左辺と右辺で反対になっている点は、同じである。つまり、7と8の位置を×記号の前後で交換しても、計算結果(答え)が同じ56、と言っている点では、どちらの交換法則も変わらない。
位置的な交換法則では、左辺と右辺で、数値だけでなく、一つ分といくつ分の位置も逆になっている。しかし、意味は両辺で同じである。つまり、右辺も左辺も、構成員数が7のグループが8つある、という数的な構造を表している。つまり、一つ分が7であることは、左辺と右辺で変わりない。
これに対して、解釈的な交換法則では、左辺と右辺で意味が違う。言い換えれば、解釈的交換法則では、左辺は構成員数が7のグループが8つある関係を、右辺は、構成員数が8のグループが7つある、という、それとは異なる数的関係を表している。つまり、一つ分が=記号の左右で、違っている。同じ7が、左辺では一つ分、右辺ではいくつ分である。数字の意味が違っている。
数学的に関心がもたれるのは、後者の解釈的交換法則であろう。位置的な交換法則は、単に、一つ分といくつ分をどこに記すか、という表記上・慣習上の問題にすぎないように思われる。実際、外国の算数教育や日本の請求書などでは、いくつ分×一つ分、数量×単価の順をよく見かける(その例外もそれなりにあるが)。
引き算では、本当は、2つの数値のうちどれが引かれる数で、他のどれが引く数で、そして、演算が引き算であるということが分かっていれば、それらを配置する順序はどうでもよいと言える。引かれる数-引く数の順は、世界的に決まっているものの、そうでなければならない必然性はなく、慣習的にそう決まっているだけである。「逆」ポーランド記号法のように、演算記号を最後に書くスタイルもある。
書き方、記載スタイルは国や文化、分野や時代によって違ってくるが、日本の算数教育の伝統では、一つ分×いくつ分、基準量×倍という順序が採用され、それでほぼ統一されている。いくつ分×一つ分という逆の順序は使わない、という点で教科書はほぼ一貫している。金額の計算でも単価×数量の順である。つまり、教科書に位置的な交換法則は現れない。いつも一つ分、単位当たり量が先である。
同じ会社の請求書、一つ一つの請求書のなかでは、この順序は統一されていた方が、誤解がない。それは教育でもそうである。統一されていたほうが、一つ分(単位当たり量)はいつも×記号の前ということで、児童にとっても、分かりやすい。教師にとっても、いちいち、どれが一つ分でどれがいくつ分かを説明しなくてもよい利点がある。
算数で教えられている交換法則は、解釈的な交換法則であり、この交換法則では、一つ分×いくつ分の順序は=記号の前後で変わっていないことに注意すべきである。解釈的交換法則では、左辺も右辺も、一つ分が前、いくつ分が後にである。×記号の前後で数値を交換しても、一つ分×いくつ分の順序は保持されるのである。したがって、一つ分×いくつ分の順序の固定と交換法則とは、両立可能なのである。
解釈的 7(一つ分)×8(いくつ分)=8(一つ分)×7(いくつ分)
算数で教えられている交換法則が解釈的な交換法則であると判断される第1の理由は、算数では交換法則は、九九表に発見できる規則性の1つとして教えられていることである。掛け算の可換性は、さしあたり、1~9(~12)までの自然数にしか当てはまらないものとして、教科書に登場する。
掛け算順序を巡る議論で、よく、「高学年で掛け算の交換法則を学んだら、順序固定は解除すればよい」といったことが言われる。「交換法則と掛け算の順序固定とは矛盾する」という思い込みがそこに働いているからである。実際には、交換法則は高学年ではなく、小学校2年生で、九九を学んでいる途中で、伏線として、すでに教えられている。たとえば、東京書籍の教科書だと、四の段のページで、4×3と答えが同じ三の段の九九は何かということが問われている。
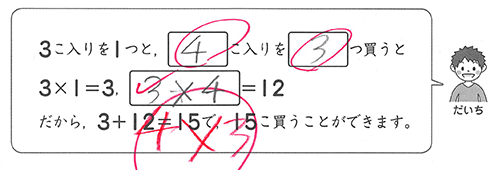
4×3と答えが同じ12である三の段の九九は、3×4である。三の段では、3個で1パックのプリンがいくつあるかに応じて、プリンの総数がどう変わるか、という仕方で、三の段の九九が学ばれる。4パックあると総数は12個なので、3×4=12。
四の段では、みかん4個が縦に積まれて、1つの細長いネットにまとめられた単位で売られていて、そのネットがいくつあるかという仕方で、四の段の九九が学ばれる。みかんネット3つでは、総数は12であるので、4×3=12である。
3×4は三の段に属し、一つ分は3つである。4×3は四の段に属し、一つ分は4である。3×4と4×3は、×記号の前後で数値を取り替えた関係にあるが、答え(総数、計算結果)は同じ12である。画像は東京書籍2下(2015) p. 17, 19から。
このことは、7×8と8×7のあいだでも当てはまる。これらは伏線だが、より一般的に当てはまる規則性として、はっきりと交換法則が定式化されるのは、九九表を完成させた直後である。これも2年生である。「交換法則」という言葉は使われず、この規則性は「決まり」と呼ばれている。
「決まり」としては、1)各段は被乗数毎に増えて行くとか、3)三の段と四の段を足すと七の段になる、ということと並んで、2)交換法則が学ばれる。つまり、掛け算では、一つ分といくつ分の数値を交換しても、答えは同じなのである。画像は東京書籍 p.41から。
7×8=8×7
左辺の7は、7の段のなので、一つ分が7である。右辺の8×7は八の段なので、8が一つ分である。両辺では、意味が違う、つまり、表している数的関係が異なる。しかし、右辺でも左辺でも、一つ分は前に置かれている。そして、両者の答え(計算結果)は56ということで、等しい。
答えは等しいが、意味(数的関係)まで等しい、とは言われていないことに注意すべきである。結果は同じでも、そこに至る過程・操作が違っている。だから、7人座れるシートが8つあるときの総人数を問う文章題では、これが表す数的構造は、したがってまた、式は、7(一つ分)×8(いくつ分)であって、8(一つ分)×7(いくつ分)ではない。
たしかに、ただ数量的に見れば、7×8と8×7は等しい。それどころか、14×4や58-2とも等しい。しかし、小学生は掛け算を、一つ分×いくつ分で学んでいるので、1つ分が違うのなら、答えが同じでも、別の事態、別の数的関係、を表していると見なされるのである。小学生においては、まだ数と意味・具体は密接に結びついている。数を純粋に、数量的な等しさにおいて抽象して扱えるようになるのは、もっと先のことである。
交換法則という言葉は使われないが、小学生は、交換法則をすでに小2で学んでいる。交換法則は、かけ算を学び始めるとまもなく、学習するのである。それなのに、なぜ、かけ算の順序を固定してかけ算を教えるのか?ということが、一見、疑問であろう。その答えは、交換法則が解釈的だからである。
黒木氏はツイッターで繰り返し、東京書籍の教科書(およびその指導書)について、交換法則が成り立つ仕組みを説明した次のページで、かけ算の順序を教えている、と非難を込めて書いている。こうした誤解もまた、交換法則が解釈的であることを見損なっているために、起きている(画像は黒木氏ツイート2017/08/22 21:48、教科書2下 2011年、p. 20, 21)。
別の教科書では、交換法則の説明に、アレイ図が用いられている。アレイ図というのは、〇印や花のアイコンなどのコマが、長方形状に揃えて配列されたものである。碁盤の上に長方形状に配置された碁石を想像すればよい。縦2横6個のアレイ図では、全部で12個のコマが整然と並んでいる。
縦2横6個のアレイ図で、縦方向に2個ずつグループ分けすると、各グループの構成員数は2で、グループの数は6である。これは式では、2(一つ分)×6(いくつ分)と書かれる。
しかし、横方向にまとまりをとると、今度は、構成員数が6のグループが2つあるので、式は6(一つ分)×2(いくつ分)。どちらも計算結果は12である。同じアレイ図なので、グループの取り方で、コマの総数が変わるはずもない。画像は教育出版(2016) p.53より。
だから、ここから次のように、交換法則が式として引き出される。
2(一つ分)×6(いくつ分)=6(一つ分)×2(いくつ分)
これは、しかし、解釈的な交換法則にほかならない。解釈的な交換法則では、左辺でも右辺でも、一つ分が先に、いくつ分が後に書かれている。2と6を交換しても、一つ分×いくつ分の順序は保持されるのである。
だから、算数で教育的に行われている、掛け算の順序の固定は、算数で教えられている交換法則と両立可能である。交換しても、一つ分×いくつ分の順序は維持されるから。それが矛盾だと感じられるのは、1つに、交換法則を位置的な交換法則だと誤解するためである。
児童は、2年生で、かけ算では被乗数と乗数を交換しても答えは同じだと学ぶが、その交換法則が解釈的であること理解しているわけではないであろう。保護者やその他の多くもそうである。位置的と区別されたものとしての交換法則として、教えられ学んでいる、というわけではない。だから、交換法則を位置的と誤認されて、逆順バツの採点に疑問を持たれるおそれはいつもある。
もう一つの原因は、数学者や数学がよくできる人たち、そして、定数氏のような数学屋に多く見られるのだが、掛け算を1つ分×いくつ分ではなく、次の言葉の式で表される直積的な掛け算として理解していることである。
因数(factor)×因数(factor)=積(product)
これは2つの集合の各要素数とその直積集合の要素数の関係である。takehikcom氏の言葉を使えば、倍志向の掛け算と区別された、積志向の掛け算である。この掛け算の逆演算は因数分解である。彼らは、かけ算の本質を、この直積的に理解された掛け算に見て、それを絶対視している。
この掛け算を説明する際にも、アレイ図が用いられるが、直積主義では、縦の数と横の数から、直接、総数を引き出し、この際に、グループ分けをしない。つまり、一つ分やいくつ分は考えない。かりにグループ分けを考えても、アレイ図の主観的な解釈、一時的に設定され、すぐに解消される仮の説明、としか見なされない。定数氏が、「教えるときに順序を設定することに反対する自由派はいない」と言うときに考えているのは、このことである。
直積的な掛け算では、×記号の前後がともに因数になっていて対称的であり、だから、そこに順序の設定のしようがない。3と4という2つの因数は対等に、12を構成している。もちろん、書くときは、2つの数値のうち、どうしても、どちらかを先に置かざるをえないのだが、その順序はまったく偶然的なものなのである。この理解では、かけ算の順序にどんな意味もない。順序がありえないところに、算数教育で順序があるかのように掛け算を教えて、児童の数学的感覚を歪めているのはけしからん、というわけである。
だが、直積主義の掛け算が唯一正しい掛け算であるという先入見から解放されれば、つまり、目が覚めれば、彼らも、矛盾でも何でもないでもないこと、黒木氏らが超算数と呼んで批判するものこそが幻影であること、に気づくであろう。
(ツイッターに2017/09/05 18:34に投稿したものを手直しした。)