A.算数に証明なし
証明は、中2で学ぶので、算数は証明は使わない。論理的思考が未発達な児童を前に、証明を行っても、無意味であろう。児童は、具体的な事物に即してしか思考できない具体的な操作期にある。そのような児童に、証明を教えようとしても、無理である。
証明がないなら、小学校では、児童に「どうしてそうなるのか」ということを理解をさせずに、天下り式に算数を教え込んでいるのかというと、そういうわけではない。具象的で直観的な仕方で、あるいは、帰納的な仕方で、納得させ、根拠づけている。
たとえば、二等辺三角形の底角が等しいことは、中2で証明されるべき最初の定理であるが、算数では、2等辺三角形の形の紙を、左右に半分に折って底角部分どうしを重ね合わせるという操作的で直観的な方法で、確認する。また、頂角と片方の底角が一致しないが、正三角形では一致することも、同じようにして、確かめる。
また、三角形の内角の和が180°になることは、下の画像のように、紙で作った三角形の角の部分をハサミで切り離して、3つの角部分を、重なり合わないように頂点を合わせて放射状に配列すると、平ら(180°)になることにより、示している。
中学では、同じことを平行線の性質を使って証明する。小学校の段階では、証明はなく、上の画像のような直観的な例示によって、三角形の内角の和が180°になることを、納得させる。
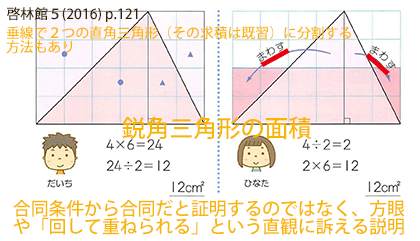
算数では、三角形の面積が、〈底辺×高さ÷2〉で求められることを習うが、底辺を横、高さを縦とする長方形の面積の半分になることは、つまり、÷2となることは、画像のように、回してぴったり重ねる、という仕方で示される。このとき、回す部分が移動先と同じ面積であることは、方眼からわかる。
鈍角三角形の場合、頂点から下ろす垂線が底辺上ではなく、底辺の延長上に下りるために、別の説明が必要となる。しかし、この場合もやはり、「回してぴったり重ねる」という操作的・直観的手法で、長方形の面積の半分になることを示している。
空氏(Twitter @musorami)は塾で小学生に、無謀にも、三角形の求積公式が〈底辺×高さ÷2〉となることを、中点連結定理などを使い、証明して見せた(202/12/31 09:47AM)。これによって、「算数の先にある数学の面白さを「感じてもら」」った、という。
カリキュラムや発達心理学への配慮がまるでない空塾ならでは許されることであるが、空氏の自己満足になっていないかどうか、検証が必要である。
算数では、定義や定理から演繹的に定理を証明するようなことはしないが、しかし、帰納的に定理を裏付けることはする。たとえば、たし算の交換法則は小2で学ぶが、交換法則の証明は、もちろん行わない。交換法則の証明は、中学や高校でも行わない。
算数では、たし算の可換性を児童にどうわからせるのか。それは、さまざまな組み合わせの2数のたし算を、+記号の前後の数を入れ替えて筆算させることで、納得させている。つまり、たし算が可換であることを、帰納的に確かめさせているのである。
数学を学ぶことで論理的思考が養われるというのは間違いないが、それは主に、公理・公準や定義から、ある命題を演繹的に引き出す証明を行うせいであろう。これは算数には当てはまらない。
B.算数に定義なし
証明だけでなく、定義についても、それが何であるかは中学ではじめて習う。中学では、「用語や記号の意味をはっきり述べたもの」のように定義されている。難しい言い方をすると、定義とは概念の内包を言葉で明確にしたものである。
たしかに、「~を…といいます」というのは、定義を与えるときに使う言い回しで、算数の教科書にも使われているが、~の部分が定義だとしても、括弧付きの(定義)だと言うべき。というのも、定義としては、いろいろな点で不完全だからである。
第1に、算数教科書における(定義)は、単なる例示に留まっているか、かなり例示に依存した説明になっている。つまり、ちゃんとした定義になっていない。定義未満の(定義)である。
たとえば、次の「上の28のような数を、わり算の商と言います」という商の(定義)は、純粋に例示で、あまりに特殊。定義は当然、一般性をもたなければならない。
次のかけ算の(定義)も単なる例示になっている。ただ、かけ算については、これに先立って、いろいろ説明があるので、この箇所だけを取り上げるのは公平ではないが、「~を…といいます」という、形式上定義である部分に限ると、このようになっている。
例示と説明が混じっている(定義)もある。たとえば、次の倍数の(定義)。「整数倍してできる数」とあって、単なる例示ではない。だが、この(定義)を文字通り受け取ると、7の倍数以外の倍数は倍数ではない、ということになってしまう。
第2に、算数における(定義)は操作的である。
たとえば、円は、中学数学では、「1点からの距離が一定である点の集まり」(東京書籍 数学3 2016年 p158)とされるが、算数では、「コンパスでかいたようなまるい形」となっている。円はコンパスを活用して描けるような図形なのである。
対称軸とは、教科書によると、ぴったりと重なるように二つ折りに折り合わせたときの折り目となる直線のこと。児童にもわかるように、折り紙を折るときの感覚に訴えているが、それだけに定義らしくない。
第3に、算数における(定義)は、定義としては、厳密さを欠き、日常的である。面積も広さのことだと書かれているが、これは日常語で言い換えただけである。「ながしかくのことを長方形と言います」と言っているようなものである。
算数におけるこのような(定義)の実態、単なる例示や方法の解説になっているような、未発達な(定義)は、しかしながら、児童の発達段階にふさわしいものとして、積極的に捉えるべきである。算数教科書では、児童の思考の発達や学習段階に応じた(定義)がなされている。
小学生は、まだ、小学生は概念語だけで論理的に考えることはできない。だから、算数のにおける(定義)も、彼らが親しんでいる日常的な自然言語や、「折る」といった日常的な操作・動作、目に見える具体的なものに拠って、数学の言葉を導入するのである。
C.長方形の(定義)
数学では、長方形は「4つの角がすべて直角である四角形」、正方形は「4つの角がすべて直角で、4辺が等しい四角形」と定義される。短く言えば、長方形は等角四角形、正方形は等辺等角四角形である。この定義に従えば、正方形は等辺である長方形、つまり、特殊な正方形である。
内包が増えると外延は減る、という論理学の原則がある。正方形は、1)四辺性と2)等角性に加えて3)等辺性をもっている。正方形は1)と2)を満たすので、長方形だが、3)を備えることで、3)の等辺性を備えない長方形が排除されることで、外延が長方形よりも狭まる。ヴェン図では、正方形の集合を表す円は、長方形の円の内部に描かれる。
算数教科書に載っている長方形や正方形の(定義)について、黒元氏は、定義として正確だと言っているが(Twitter 2021/01/31 03:27PM)、それらの(定義)が本当に定義なのか疑わしい。
それとも、他の(定義)は定義未満だが、長方形や正方形の定義だけは立派な定義である、なんていうことがあるのだろうか。まず、「かど」という日常的な言葉を使っている点では、定義らしくない。それは定義ではなく(定義)にすぎないのではないか。
長方形については、「4つのかどがみんな直角になっている四角形」と書いてあるが、実は、「角がすべて直角である【が、隣り合う辺が異なる】四角形」という排反的な定義の、【 】内の細かい部分を小学生向けに省いた(定義)である可能性もないとは言えない。
実際のところ、その定義の脇に長方形の例として描かれているものは、すべて、縦と横の長さが異なる長方形なので、このような推測は的外れだということはないであろう。文章による説明と描かれた図形とが一体となって、長方形を(定義)している。
だとしたら、ここから「正方形は長方形である」ことを導き出すことはできないであろう。もしそれが本当に定義だとすれば、そこからはそのような帰結が引き出せても、定義未満の単なる(定義)からは引き出せないのである。
算数教科書では、A)長方形の定義は包摂的なのに、B)いくつかのタイプの設問や言い回しから、「長方形」は排反的に理解されていて、そのあいだに矛盾があると言う者もいる。
その設問の代表は、描かれたさまざまな図形から長方形を記号で選ぶ設問。その模範解答には、正方形の記号は含まれていない。
また、縦横が同じ長さで高さが異なる直方体の面の形とその数を答える設問では、模範解答は、長方形が6つでそのうち2つが正方形なのではなく、長方形が4つ正方形が2つ、となっている。
しかし、A)とB)のあいだには、本当は、矛盾はない。というのも、これまで見てきたように、A)で言われている「定義」は実は、定義ではなく、(定義)にすぎないからである。かりに定義であるとしても、小学生のほとんどは、そこから「正方形は長方形である」、「正方形は長方形の特殊な場合である」という、正方形と長方形の包摂関係を引き出せないであろう。
現代化の時代(1970年代)には、小学生に、集合概念やヴェン図を用いて、図形の包摂関係が教えられた。長方形の(定義)は現在と同じである。しかし、ほとんどの児童はその包摂関係を理解できなかった。
というのも、小学生はまだ、定義から論理的に推論する論理的思考力が発展途上だからである。小学生は、図形を多分に、視覚的イメージや日常的自然言語で把握しようとする。児童は(定義)よりも、教科書の長方形の(定義)文の脇に描かれた図形を手がかりに、長方形を把握している。
イメージとしては、正方形と長方形は、かどが直角で似たところもあるが、一方は長いが他方は長くないといった異なるところもある、2つの異なる四角形である。日常語でも「インスタの写真は正方形がいい?それとも長方形?」のように言われ、両者は排反的。排反的ではあるが、論理的に排反としてはっきり規定されているのではなく、前論理的に排反的なのである。
論理的な包摂関係の理解は、小学生に一般に難しいので、論理的な思考が発達する中学生になってはじめてその関係は教えられている。現在の小学校では、教えられていないので、小学生は視覚的イメージや日常言語の用法に従って、両者の関係を前論理的な仕方で、排反的に考えている。
そして、教科書の記述や設問も、それを前提として作られているのである。算数教科書では、「正方形は長方形である」とも、「正方形は長方形ではない」とも、はっきり、書かれていない。ただ、その表現や設問において、前論理的な排反性が暗に前提とされていると読み取れるだけである。