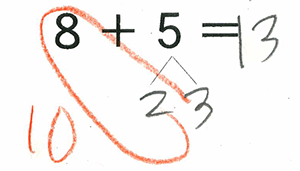New Math運動の失敗
1957年にソ連が世界初の人工衛星を飛ばすことに成功すると、米国には激震が走った。スプートニックショックと呼ばれる出来事である。科学技術において米国は最も先進的だという信念が、崩れ去ることになったのである。当時の米国の数学教育が旧態依然であったことは、米国がソ連に追い越された原因の1つと見なされ、1960年代、New Math運動と呼ばれる、数学教育の「改革」運動が起きた。現代の数学の発展を受けて、数学教育を現代化しようという運動であった。
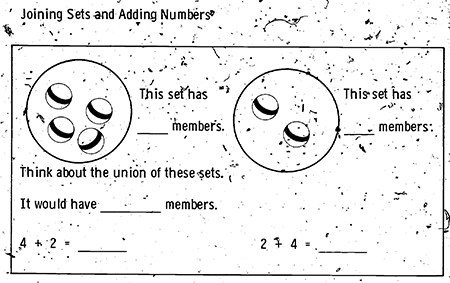
現代化の時代、小中学校の数学では、集合概念や、写像としての関数、位相幾何、公理主義化された代数が教えられた。集合論や公理主義は、単に、新しい単元として加えられたのではなく、数学の基礎、枠組みとして、採用されたのである。New Math運動の主要な担い手の1つであったSMSG (School Mathematics Study Group)の教科書を見ると、小1から、数や足し算が集合で定義されている。その初っ端が集合概念の導入である。果物の集合(set)には、リンゴの集合やナシの集合など、部分集合(sebset)がいくつもある。リンゴの構成員(members)の数は5である。つまり、数は集合の要素の数なのである。マルで囲って、リンゴ2つと梨3つの部分集合を作ることも可能である。
(SMSG, Mathematics for the Elementary School, p. 2)注1
足し算は、後のほうのページで数直線を使って説明されるが、最初は、やりは集合から説明される。4つのボールから成る集合と2つから成る集合があって、両者を合わせてできた集合(union)の要素は6である。そこから、4+2=6, 2+4=6という足し算の式が導かれている。
(p. 9)
集合概念を使って足し算を考えると、物がそれが置かれている場所と時間から抽象され、頭の中で、同じ定義を満たすものとして集められる。このような理解をすると、算数教育学で言う合併(あわせて)と増加(ふえると)の違いは、無意味なものとなる。特定の場所に最初からあったかどうか、追加されるものは最初からあるものより後という時間的な前後関係は、捨象されるからである。
New Math批判の書『ジョニーはなぜ足し算ができないのか』には、New Math教育がどんなものであったかを示す例が、冒頭に書かれている。
「現代の数学のクラスを覗いてみましょう。……教師は「6と9のあいだにある整数は、正しくは、どう表現するの?」ときくと、ある生徒が「なぜ? 7と8だよ」と答える。教師は「いいえ、6より大きい整数の集合と、9より小さい整数の集合の交わりとなる整数の集合よ」と答えた。」 (注2)
New Mathの数学のテキストや授業は、こんなものなのである。数学者の小平邦彦は米国滞在中に娘が、SMSGの実験クラスに配属されるという災難に見舞われた(注3)。彼はその宿題の手伝いをやらされ、その馬鹿らしさに呆れて、現代化数学に批判的な論者の1人となった。
小平は言うのだが、集合の考えは数学者には分かりやすく基本的だと感じられるが、それは専門的訓練の結果であって、小中学生にとってそうではない。集合論が現代数学の基礎であるからと言って、集合論が数学「教育」の基礎ということにはならない。集合論は19世紀末になって初めて出てきたものだが、数学はそれより2000年以上も前からある。つまり、歴史的に見れば、数学が集合概念を基礎に再構成されたのは、数学にとって、偶然的な出来事なのである。現在の近いほど数学は抽象的であり、小中学校では、直観的にわかりやすい過去の数学から学んでいくべきだと言う(注4)。
New Mathで算数を学んだ子どもたちがどうなってしまうかを、象徴的に示す例を2つ挙げよう。1つ目は、スヌーピーで知られる、シュルツ(Ch. M. Schulz)の4コマ漫画である。チャーリーブラウンの妹サリーは、New Math時代の教科書を教室で読んでいる。「集合、一対一対応・・・等価な集合・・・集合を結びつけて1つにすること・・・」 しかし、最後に(4コマ目で)こう叫ぶ。「私が知りたいのは、ただ、2たす2はいくつか、ということだけよ!」。
2つ目は、先ほど言及した『ジョニーはなぜ足し算ができないのか』に描写されている、New Mathで算数を習う子どもと親とのあいだの、よく知られた会話である。
「子どもの算数の学習の進度を心配した両親は、子どもに尋ねる。ある父親が、8歳になる自分の子どもに、「5たす3は何?」と尋ねた。親が受け取った答えは、「交換法則により、5 + 3 = 3 + 5 」というものであった。面食らった親は、同じ質問を言い換えて、「5つのリンゴと3つのリンゴ、併せると全部でいくつ?」ときく。子どもは、「と」がプラスの意味なのかよく理解できなかったので、親に「5つのリンゴ、プラス 3つのリンゴ、ということ?」ときき返す。急いで「そうだ」と答えて、期待して子どもの答えを待った。子どもが答えて言うには、「リンゴだろうが、ナシだろうが、本だろうが重要じゃないよ。どの場合でも、5 + 3 = 3 + 5だよ」」(注5)
このように、New Mathで算数を学ぶと、集合の用語・記号法や交換法則は知っていても、九九を覚えられず、基本的な計算ができなくなってしまう。New Mathの数学教育がいかに偏っていたかが分かる。
現代化算数と集合概念
このNew Math運動は世界的に波及するが、日本もその波をかぶることになった。1964年にはSMSGが数学教育会や雑誌で紹介され、セミナーも開かれた(注6)。穏健化された形ではあるが、10年ほど遅れ、1970年代の日本の小中学校で、現代化のカリキュラムが実施された。図のように、小4の教科書には、集合に関する単元が出てくる。
(大阪書籍算数教科書4下、1977年、p. 4)
この集合概念に基づいて、さまざまな四角形の集合のあいだの包摂関係が、ヴェン図で示された。それによれば、正方形の集合は長方形の集合の部分集合である。というのも、等辺等角四角形である正方形には、等角四角形である長方形の性質が完全に当てはまるから。つまり、正方形は長方形の特殊な場合なのである。
さらに言えば、正方形の集合は、等角四角形である長方形と、等辺四角形であるひし形という2つの集合の交わり(積集合)に当たる。長方形の集合は、これはこれで、平行四辺形の集合の部分集合である。このように、さまざまな四角形のあいだには、現代化時代の教科書に載る次のようなヴェン図で示される包摂関係が成り立つのである。
(啓林館算数教科書6下、1973年、p.86)
集合とは、大阪書籍の教科書によれば、「ある事柄に当てはまるものの全体を、1つの仲間と考えたとき、その集まり」と定義される。
だが、小学生が集合概念をどれほど理解できたであろうか。「集まり」ということで、小学生は、一箇所に寄せ集められてできた玩具の山のようなものを、まず連想していないであろうか。ある小学生は、運動場に足で大きく円の形に線を引いて、同級生とともにその中に入り、「全員集合!」と叫んで、これが集合だという理解を示した。また、「なかま」という言葉が集合の説明に使われているが、仲間だったら普段よく遊び、互いによく知っているものどうしの関係でないといけないであろうか。もし、当時の児童たちの集合概念の理解がこんなものであったら、無限集合の理解はおろか、有限集合の理解でさえも、不可能である。(注6b)
集合の要素は、実在物でも空想物でもよく、過去・未来のものでも、数や図形でもよい。たとえば、血液型がRhマイナスの人の集合では、血液型がRhマイナスであるという条件を満たしていれば、すべて自動的に、その集合の要素である。頭のなかで考えられた集まりなので、Rhマイナスの人は、互いに相知らず、隔たったところに居住していても構わないのである。100年前に死んでいても構わない。200年後に生まれるRhマイナスの人も含まれている。人間の部分集合であれば、弁理士だとか、~小4年1組で兄がいる人だとかいった、決まった特徴を共通してもち、それを持たない者と区別される諸個人のグループを頭のなかで想定するとき、それがすでに集合である。集合は、要素間の物理的な近接性や緊密な関係の有無とは関係なしに、人間の頭のなかで自由に構成されるものなのである。
しかし、小学生は、目の前のお皿の上の青森産のリンゴが数えると5つあるとか、自分が自宅の近くの小学校の4年1組に属し、誰々と一緒の班に属しているとかいった、実在の融通が利かない具体的な状況に即して、物を考える。物理的遠近や実際の具体的な関係から独立に、ある特徴や観点に基づいて事物や人、項目を自由にグループ化し、それらの間の関係を考察するような、高度な抽象的思考力を、最初からもっていない。むしろ、そのような能力は、小学校・中学校の勉強などを通じて、次第に養われていくものである。
現代化時代の児童たちの悲惨
正方形が長方形であること、正三角形が二等辺三角形であることに、教えられずに自発的に気づく子どもがいるであろうか。いても、きわめて稀であり、無視してよいと思う。しかし、現代化の時代には、それが教科書に書かれ、教えられていた。図形の包摂関係を理解できた児童は、少数にしてもいたのであるが、ほとんどの児童は理解できず、混乱が広がった(注7)。
まずは教師の側からの証言を見よう。ブログ「身勝手な主張」のブログ主Y.H氏は、現代化算数時代に新任教師として小学校で教えていた。当時、ブログ主が「正三角形が二等辺三角形のなかまである」と児童に教えたら、児童のあいだで大混乱になったと言う。
「私が小学校の新任教師をしていた頃は、数学教育の現代化の時代であったから、当然「正三角形は二等辺三角形のなかまである」と教えていた。……私の教え方がよくなかったのかどうかわからないが、「正三角形は二等辺三角形のなかまである」が児童の間で大混乱になった記憶がある。」(注8)
図形の集合論的な分類方法は、明らかに、小学生の図形イメージとそれに基づく自然な分類に反するものであった。だから、Y.H氏は平行四辺形については、次のように書いている。「第一、無限にある長方形をどのように「長方形の集合」として閉曲線で囲まれたベン図に押し込めるのか?こんな冗談みたいな思いを持っていた。実際、児童の混乱もひどかった。
長方形を平行四辺形として見よと言われても、児童は長方形と平行四辺形のそれぞれの図形としてのイメージがあって、別のものと思うのが自然な思考であって、無理な話であった。長方形や平行四辺形が数学的にきちんと定義されていない算数では、このような見方は飛躍がある。」 (注9)
次に、現代化算数を受けた児童の側からの証言を聞こう。読売オンラインの発言小町で、2014年に、「小学校 正方形が長方形でないのはなぜ?(駄) 」というトピが立てられたことがある。(注10)
そこにredbearという人が投稿していて(2014/11/15 20:31)、自身の40年以上前(1974年以前)、つまり、現代化算数が教えられ始めた時代の体験について語っている。redbearさんが小学生のとき、算数の時間に「長方形は平行四辺形である」という問題が勃発した、というのだ。redbearさんだけが「長方形は平行四辺形である」と主張し、他の全員が反対で、redbearさんは集中砲火を浴びる。反論できなかったredbearさんは、翌日、反論の仕方を考えてきて発表した。そして、数学が専門の担任によって、redbearさんの主張が正しいという裁定が下されたのである。
これは、現代化算数が始まって日本全国の教室で起きていた混乱の1コマに過ぎない。琉球大学の色物氏も、readbearさんと同じ年代で、「「正方形は長方形に入るか」で議論して同級生を泣かしたことがあった」と、いじめを告白している(ツイッター 2010/11/13 09:24)。理解できた極めて少数の児童と、理解できない多くの児童に対立と分断が起きたのである。授業についていけない多数の落ちこぼれと算数嫌いの児童が続出したのは、言うまでもない。
redbearさんのクラスでは、redbearさん1人を除くと、児童は、「長方形は平行四辺形である」という命題を理解できなかった。図形の包摂関係の理解は、小学生の知的枠組みを超えており、小学校で教えるには、明らかに不適切であった。外国での流行に乗って、小学校で集合を教える現代化カリキュラムを導入し失敗した事件は、日本の教育政策史上の汚点となっている。小学生に対する知的虐待が制度的に遂行されたのである。当時小4で教えられていた集合の概念は、今は、高校生が学んでいるのである。(注11)
集合論的観点の持ち込み
四角形のあいだの多層的な包摂関係は、その理解が小学生の知の地平を超えているので、算数で教えるのは不適切である。では、どう教えるかと言えば、中学では包摂関係を教えるので、円滑な小中接続のことを考えれば、小学校では、現行のように、四角形間の包摂関係を曖昧なままにせざるをえないであろう。では、正方形と長方形の包摂関係についてとくに何も述べなければ、小学生は両者の関係について皆目わからないかというと、そうではなく、児童の頭の中では、常識と日常言語に基づいて並列的に解釈されるであろう。
日常的な理解では、正方形(真四角)は長方形(長四角)とは別のものである。断面が正方形と長方形の2種類のレールがあるとき、「長方形のほうを取ってきてくれ」と頼まれれば、あえて正方形のほうを持ってくる人はいないであろう。児童たちは、生活のなかで獲得されたこの常識的な理解に従って、正方形と長方形を、さまざまな四角形のなかの2種類として、あい並んでいるものとして理解している。教科書では、たとえば、正方形の面積の公式(一辺×一辺)は長方形(縦×横)とは別立てになっているのであるが、これも日常的言語の用法に従うもので、長方形を「等角だが等辺ではない」とするユークリッド的な定義(注12)を積極的に主張しているわけではない。
算数では、さまざまな形の四角形を図示して、たとえば、長方形と呼べるものの記号を全部挙げよという、下のような設問がしばしば出る。このような設問では、正方形の記号を選ぶ可能性は、考えれておらず、模範解答でも、正方形の記号は書かれていない。このことから、小学校では、「正方形は長方形ではない」と教えられている、といった解釈がなされ、批判されることがある。だが、これは図形の包摂関係についての理解と知識を基準に、小学生向けのこの設問を理解したために生じた歪んだ解釈である。問題作成者はそのような包摂関係を前提としてこの設問を作成したのではない。
(光文書院3年生夏休みドリル p.3から)
確かに、小学教科書では、長方形は4角が直角の四角形、正方形は4角が直角で、4辺が等しい四角形と定義されている。この定義に従えば、算数でも、正方形の集合が長方形の集合の部分集合になるのではないのか。だが、定義から集合的包含関係を引き出すためには、定義と真の命題の違い、内包を増やすと外延が広がるといった概念の内包と外延の関係などを理解していないといけない。だが、そのような論理学的知識は、2年生にはまだない。ましてや、主語概念の集合が述語概念の集合の部分集合のとき命題が真と言えることを知っていて、「正方形は長方形である」と言える小学生は、まずいない。「正方形は長方形である」ときくと、小学生は、正方形=長方形と理解するであろう。
(東京書籍算数教科書2下、2014年、p.104, 105)
だから、上記のような、図形の記号を記入する問題が出ても、長方形の欄には、正方形ではない長方形のみを「全部」選んで入れるのが正解である。もし、正方形の記号(○ア、○ク)を含めれば、それは、「「正方形は長方形」と理解していたからマル」なのではなく、両者の区別さえついていないからバツになるだけである。
四角形の集合の包含関係が既知・既習で自明であるような後知恵的・鳥瞰的な視点から見ると、たしかに、その名称の四角形を選ぶ設問、および、その採点方針は、正方形を長方形の一種とする定義を否定しているように見える。しかし、包摂関係はここでは一切、問題にされていないと銘記すべきである。この設問を評価するとき、その知識の適用は一時停止しなければならない。
ところが、このことを理解せずに、中学で学ぶ図形の集合的包摂関係を金科玉条のように振り回して、「算数では嘘が教えられている」と、算数教育を批判する者がいる。彼らは、中高で学ぶ図形理解を、小学校の算数教育に関する話の中にそのまま持ちこんで、これを基準に、小学校の授業や設問を批判してしまう。だが、そこで、図形についての集合的理解に基づいて、長方形はどれかという設問に正方形を含めて解答する子どもと想定されているのは、実は、彼ら自身にほからない。これは何度でも強調されるべきだが、算数の問題は小学生が解くべく与えられたものであり、数学が趣味の大人や数学塾講師のために作問されたものではない。小学校では、四角形の仲間として、正方形や長方形、ひし形、平行四辺形、台形があることを知り、それらの主な特徴を知り、その典型的なイメージに基づいて互いに識別し、その典型的な形をノートに描ければ、それで十分である。
算数の採点答案がネットで論争を呼ぶ多くの場合、その原因の多くは、上の学年や高等数学で学ぶことを、無意識に持ち込んでしまうことにある。小学生にも容易に理解しうる、理解されていると安易に前提してしまうのである。ツイッターの"掛算"、"超算数"タグで批判されている多くの場合が、これである。小数の足し算の筆算の採点を、中学で学ぶ有効数字を根拠に子どもへの虐待だと騒いだり、小学教科書での偶数・倍数の定義を、高校数学や初等整数論の定義に基づいて「ひどい」と評したり、小2のかけ算の式の書式の順番を、直積的なかけ算の意味を基準に可換性の否定と断じたり、といった倒錯的なことが起きている。
小学校の教科書の、長方形を初めて説明するページに、長方形の例として描かれているのは、縦横の長さがはっきり違う典型的な長方形である。正方形が長方形の特別な場合だとしても、そこに、正方形が描かれることはない。
(上図)東京書籍2上104、(下図)、4上64
同様にして、台形を定義し説明する箇所では、台形の例として図示されているのは、やはり、上辺と下辺の長さが異なる典型的な台形であり、正方形やひし形、平行四辺形ではない。上辺と下辺が平行といった図形の特徴とともに、こんな図形が台形だというイメージが捉えられていればよい。
描かれたさまざまな図形から、その名称の図形を選ぶ、上記のような問題において試されているのは、単純なことで、教科書に載っていたような典型的な四角形のイメージが頭に入っているかどうか、言い換えれば、教科書に載っていたような形の図形は、何と呼ばれていたか、である。さまざまな四角形の集合のあいだの包摂関係など、微塵も問題にしていない。
「児童は長方形と平行四辺形のそれぞれの図形としてのイメージがあって、別のものと思うのが自然な思考」(Y.H氏)なのである。
関連記事
注
注1 SMSG, Mathematics for the Elementary School, Book 2, Studtent's Text, New Haven / London, Yale University Press, 1965.
https://archive.org/stream/ERIC_ED173089#page/n9/mode/2up
注2 Morris Kline, "Why Johnny Can't Add"
http://www.marco-learningsystems.com/pages/kline/johnny/johnny1.html
Morris Kline, Why Johnny Can't Add: The Failure of the New Math, St. Martin's Press, 1973. 日本語訳『数学教育現代化の失敗』(柴田録治訳、黎明書房、1976年)
注3 「SMSGの濫觴時代に私の長女がアメリカのプリンストンの中学校でその教育実験の級に編入され、私は奇妙な宿題の手伝いをさせられる破自になった。おかげでSMSGの馬鹿らしきは身にしみているのである。」
小平邦彦、『怠け数学者の記』(岩波書店、2000年)、p. 117. Vgl. p. iv, 110.
注4 小平邦彦、『怠け数学者の記』、p.120. 小平によると、集合論は有限集合に限定するなら、一見易しく見えるが、これが間違いのもとである、という。集合論や公理主義代数のうち、子どもたちも理解できる非本質的な部分、とてもつまらない部分が教えられた。子どもたちには、それはとてもつまらない、無意味なものに見えた。ともかく、そのような非本質的な部分に多くの時間と労力が無駄にかけられることになったために、子どもたちは、この年齢期に基礎的な計算力を身に付けてしかるべきなのに、それを得る機会を逸してしまったのである。
「現代の数学は集合論の影響を強く受けていて、集合論が数学の基礎であると考えるが、集合論が創まったのは一九世紀も終りに近くなってからであって、数学は集合論が創まる二〇〇〇年も前から存在していたことを忘れてはならない。」 p. 111
「進歩発展するものの典型的なものは生物であるが、生物の「個体発生は系統の進化を繰返す」ということがある。同様に、数学の教育も数学の歴史的発展の順序に従って行われるべきであろう。」 p. 111
「数学者は集合が基本的なわかり易い概念であると考えるが、それは多年の専門的訓練の結果であって、それを忘れて、物の数を数えるという操作は集合の一対一対応に基づいている等と言っても、子供は仲々納得してくれないのである。」 p. 112
「new math流の教科書には現実の子供よりも数学者の頭の中に描かれた子供、言わば公理化された子供を対象としている傾向があると思う。子供から見た数学の難易の順序は、その論理的順序よりも歴史的発展の順序によると思うのである。」 p. 115
注5 Morris Kline, "Why Johnny Can't Add"
注6 竹村弘・小川庄太郎・安達徳治、「数学教育の現代化について(Ⅰ)」 『奈良学芸大学教育研究所紀要』第1巻(1965年)、pp. 36-55.
http://near.nara-edu.ac.jp/bitstream/10105/6094/1/ier1_36-55.pdf (奈良教育大学学術リポジトリ)
注6b 教師が黒板に大きく丸を描いて、そのなかにいくつかの形が違う三角形を描き、これが三角形の集まりだと言ったところ、ある1年生は、そのマルをはみ出るさらに大きな三角形を描いて、三角形の集合に入っていない三角形の存在を指摘した。山本忠「昭和40年代の小学校算数科における現代化教材に対する再評価の観点」『名古屋女子大学紀要(人文・社会編)』第63号 pp. 207-216; p.210.
ある子どもは、自分と自分の兄弟の周囲に括弧{ }がないから、集合ではない、と主張した、という。小平『怠け者の記』 p.111
どちらも、運動場に大きな円を描いてその中に同級生とともに入って「これが集合だ」と言った小学生と同様に、ベン図の囲い線や列挙法の括弧などを、集合の要素と同じ実在の平面で理解しようとしている。
注7 数学者の松崎克彦氏は、「「ましかく」も「ながしかく」」という短い伝記的文章のなかで、現代化算数との出会いについて、印象深い文章を書いている。
http://www.math.ocha.ac.jp/~matsuzak
氏は1963年生まれということなので、ほぼ、現代化時代に算数を学んだ世代である。当然、当時は、正方形は長方形の一種として教えられていた。さまざまな図形が描いてあって、「その中から長方形を選べ」という問題が出たら、正方形も含めなければならなかった。松崎氏は「指導要領が小学校低学年の子供にこのようなことを要求していたとも思えない」と書いているが、しかし、集合概念を組み込んだ当時の現代化カリキュラムは、まさに、小2にそれを要求していたのである。当時の指導書には、正方形を等辺の長方形として教えるということが書かれている。
「正方形については、長方形のうちで、四つの辺の長さが等しいものであるという見方もとれるようにするなど、将来、それらの包摂関係を理解するのに妨げにならないように注意していることもたいせつなことである。」(『小学校指導書算数編』 文部省 1969年5月 p.67)
ところが、算数のテストでほとんど百点以外をとったことがなかった松崎氏は、この設問で正方形を挙げずに、減点をくらってしまう。その理由が分からず、先生にきいたところ、長方形は「すべての角が直角であるような四角形」と定義されるが、これは正方形にも当てはまる、というのであった。このことは松崎氏にとって、思考発達上の重大な出来事となったようだ。それ以降、氏は用語の定義やルールの明確化ということに注意深く、そして神経質になった。松崎少年は、主にイメージで図形を理解する思考から脱却して、定義に基づいて図形間の関係を考える論理的な思考を獲得したのである。
ここでは、算数のテストは百点以外が稀で、しかも、のちに数学者になった松崎氏さえ、図形の問題で正方形を挙げずに減点された、という事実が重要である。それほど、図形間のあいだの集合的包摂関係の理解は、小学生に負担を与える、ということなのである。
注8 Y.H氏「新しい算数教科書『たのしい算数』2 ~三角形・四角形の取り扱い」(2015/4/17)、ブログ「身勝手な主張」内
http://blog.goo.ne.jp/mh0920-yh/e/fc74b3c22515e31359e53733bc4ae0c2
注9 Y.H氏「数学教育の現代化の時代 ~現在の算数教育で、「集合」教材の追放はどうであろうか?」(2013/11/22)、、ブログ「身勝手な主張」内
http://blog.goo.ne.jp/mh0920-yh/e/7bd57bda04a22c1052150495202267ac
「無限にある長方形をどのように「長方形の集合」として閉曲線で囲まれたベン図に押し込めるのか?こんな冗談みたいな思いを持っていた。」というところを見ると、Y.H氏自身が、集合概念を理解していなかったということであろうか。だとしたら、氏から教わった小学生はますますわからない。
図形の包摂関係を教えて児童に混乱が起きたという、この経験から、ブログ主のY.H氏は、児童のレベルを無視してすべての児童に一律に、そう教えることに反対している。しかし、正三角形が二等辺三角形であることに気づく児童の発想まで、バツを付けることで否定すべきではないとも、書いている。また、集合概念自体は、有限集合に限定するなら、小学生にとって理解可能としていて、それを算数の教材から排除したのは誤りとしている。
私の考えでは、包摂関係に気づく児童を想定することは、まさに、「数学者の頭の中に描かれた子供」、自分自身の能力を投影して創作された子どもを想定することである。また、集合概念は、有限集合に限っても、小学生にはその理解が難しいであろう。
注10 「小学校 正方形が長方形でないのはなぜ?(駄) 」(トピ主:たぬき)、読売オンライン発言小町内
http://komachi.yomiuri.co.jp/t/2014/1114/689149.htm?o=0&p=0
注11 集合の概念を学ぶのは高校の数学Aにおいてだが、中学の教科書にすでに、自然数・整数・有理数、正方形・長方形・平行四辺形などのあいだの包摂関係を示すヴェン図が載っている。だが、中学校で、これが理解できない生徒が多数いて、数学教育に困難を来している、という話はきかないので、中学生くらいになると、図形間の包摂関係はわかる、ということであろう。小5,小6くらいに、論理的な思考が発達するためだと思われる。
(修正的追加)[と書いたのだが、次の論文を読むと、どうも、中学生にとっても、四角形の階層的分類は難しいらしいことが分かった。
Masakazu Okazaki and Taro Fujita, "Prototype Phenomena and Common Cognitive Paths in the Understanding of the Inclusion Relations Between Quadrilaterals in Japan und Scotland"
http://www.emis.de/proceedings/PME31/4/40.pdf
この論文の著者に限られないが、教育心理学者たちは、理解するのが困難な図形の包摂関係を、いかに効果的に教えるのかということに関心がある。私としては、それらの研究の出発点となる「理解するのが困難な」というところに注目したい。
van Hieleによると、図形の理解は5つの段階を踏む。第2段階では生徒は、各図形の諸特徴をつかみ、第3段階で各四角形の定義と特徴に基づいて、長方形は平行四辺形の特別な場合であることを演繹できるようになる。
ところが、研究では、第2段階から第3段階への歩みは遅く、中3でも多くの生徒が、第2レベルに留まったままなのであるという。中二氏の言っていることは誤っている。図形の包摂関係は中学生にとってさえ難しいのである。
"the classification of quadrilaterals by inclusion has been shown to be a difficult task (de Villiers, 1990, 1994)." p. 4-41. 「包摂による四角形の分類は、難しい課題であることが示されてきた。」ただし、ある包摂関係は他より理解しやすい、といった図形による違いはあるという。
T. Fujitaらが参照しているde Villiersの文献の1つは
De Villiers, M. , "The role and function of a hierarchical classification of quadrilaterals", For the Learning of Mathematics, 14(1994), pp. 11-18.
De Villiers自身も、ここで、先行研究を示しながら、次のように言う。「過去何年にも渡って行われてきた、Van Hiele理論についての多くの研究が、多く生徒が、四角形の階層的分類について困難を感じている、ということを、明白に示してきたのである。」(p. 17)
"Many studies on the Van Hiele theory over the past number of years have clearly shown that many students have problems with the hierarchical classification of quadrilaterals [e.g. Mayberry, 1981; Usiskin 1982; Burger & Shaughnessy, 1986; Fuys, Geddes & Tischler, 1988]." p.17]
学習指導要領が改訂され、現代化カリキュラム(1971-1979年)の時代が終わると、集合についての章や集合概念を使った記述は教科書から消滅したが、図形の包摂関係については、第2次ゆとりカリキュラムまで残った。1985年の学校図書の教科書には、封筒から長方形の色紙を少しずつ出していくという直観的な例示に基づいて、正方形は長方形の特殊な形と言われている。正三角形と二等辺三角形、長方形と平行四辺形の関係についても、似たような仕方で、示されている。
注12 ユークリッド原論では、長方形は、「すべての角が直角だが、ただし、等辺でない四角形」とされている。原論は西欧では永く、幾何学の教科書として使われていたので、西洋人にとって、長方形は正方形とは別物であった。だが、彼らは永いあいだ、ずっと間違ったことを信じていたのであろうか。
(The First Six Books of The Elements of Euclid, trans. by Oliver Byrne, London, 1847; xxi. URL: publicdomainreview.org)
しかし、これは定義の違いの問題にすぎない。もちろん、ある定義は多くの人が採用していたり、学界で確立したものであったりするであろう。あるいは、その定義のほうが都合がいい、ということで採用されていることもある。そのような、支配的ないし都合がいい定義がわかっているかどうかが試されているという学習的状況では、それと違う定義を挙げることは、「間違っている」と判断される。
しかし、原則を言えば、定義は、任意に決めることができるので、根本的には、定義に正しいもまちがいもない。確かに、「すべての角が直角な四角形」という定義のほうが、「すべての角が直角な、ただし、等辺でない四角形」よりも、但し書きがないので、シンプルで、数学者が好むであろう。ただやはり、正方形との関係が複雑になるという欠点はある。正方形である長方形と正方形でない長方形が存在することになる。これに対して、ユークリッド的定義はこの問題点がなく、正方形や他の図形は、重複なしに、明確な境界線ではっきりと区切られている。
だから、集合論が基礎となっている現代数学のスタイルの定義と、ユークリッド的定義のどちらが優れているかは、簡単には決められない。
補遺
定数氏の掲示板へのTaKu氏の書き込みから知った論文
三木崇正他「算数を学び続ける児童を支える授業に関する研究 : 定義から図形を捉える活動を通して」(「鳴門教育大学授業実践研究」16, 2017.5)
http://8254.teacup.com/kakezannojunjo/bbs/t47/317
著者たちは、付属小4年生を対象として、正方形に長方形やひし形の定義(決まり)が当てはまるかどうか確かめさせることで、正方形を単に長方形またはひし形とは別の四角形としてとらえる理解を超えさせることに成功した。 実験的授業では、正方形が長方形の決まりを守っているかという問いに対する反応で、わずか児童の20%しか肯定しなかったが、正方形がひし形の決まりを守っていると答えた児童は80%もいたという。この違いは、長方形に関する質問のあとでのディスカッションで、児童たちのあいだで、定義から図形を判断する能力が養われたからである、という。
しかし、これによって、正方形がひし形と関連づけられただけである。つまり、著者たちの考えでも、こうした授業にもかかわらず、児童たちは、正方形の集合をひし形の集合の部分集合とするような包摂関係までは理解したとは言えない。だから、論文の結論には、次のように書かれている。
「(※現在の算数教育では教えていないので)児童は定義と性質を区別することができておらず,正方形,長方形,ひしがたの3つの図形の包含関係を正確に理解するまでには至らなかった。」(p. 69)
TaKu氏は、なぜかこの論文を、包摂関係を理解する児童がいることの証拠として挙げている。包摂関係を教えた現代化算数の時代でも、理解した児童はいたにはいたであろう。理解できない級友をからかっていた色物氏はその例である。しかし、この論文によって示されたのは、むしろ小学生には図形の包摂関係の理解が難しい、という真実の再確認である。
(2018年1月19日18:16 などのツイートに基づく)