1.1950年代
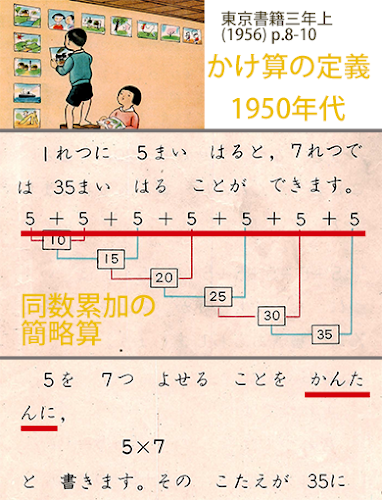
1950年代、日本では、かけ算は、同数累加(repeated addition)の簡略算として定義されていた。この定義は国際的でかつ伝統的なもので、ユークリッドの原論にも見られるものである(注1)。
つまり、5+5+5+5+5+5+5と同じ数を5つ足すことを、繰り返される対象となった数(被乗数)と繰り返しの回数(乗数)の2つの数を用いて、簡潔に5×7と表記したのが、かけ算である。
つまり、この定義だと、かけ算はたし算(当時は寄せ算と言った)の特殊な場合にすぎない。この定義では、乗数が小数になったときに困難が生ずる。5を7回足す(寄せる)ことはできるが、7.5回足すことはできない。
また、この定義だと、乗法は加法のと特殊な場合のための特殊な表記法ということにすぎない、ということになってしまい、乗法に四則演算の1つとしての独立性を与えることができないうらみがある。
この定義はたし算を基礎としているので、たし算既習の小学生には、理解可能なはずであるが、定義自体は、式の表記上システムの話なので、小学生には、納得して理解してもらうことは難しかったかもしれない。というのも、小学生は、抽象的思考が未発達で、具体的な事物や動作からこそ物事を理解できるからである。
だが、この定義では、5+5+5+5+5+5+5という式の各項(5)の下に、5つのリンゴが載った皿を7つ描くことで、複数の同数グループの具体物に対応させ例示することが容易である。対応させることで、一つ分×いくつ分による現在の定義との違いはあまりなくなる。
小学生にとって形式的で理解しにくいという、この定義の問題点は、十分に例示すれば、解消可能である。
2.1960年代~1970年代
生活単元時代(1950年代)は同数累加で定義されていたかけ算は,次の系統学習時代(1960年代)に,倍で定義されるようになった。
この定義は、戦前の緑表紙教科書におけるかけ算の定義を踏襲するものである。系統学習の教科書は,実際、緑表紙教科書を手本としていたのだから、当然である。かけ算に入る前に,テープや図形を使って,倍を定義しておく手法も,緑表紙由来である。
続く現代化時代も,かけ算の定義については変化はなく,倍による定義であった。SMSGの教科書のように,アレイ図と直積で定義するような極端に走ることはなかった。
倍がどういうことかは,学校図書では,緑表紙と同様に,かけ算の章の少し前のところで,説明されている。テープを半分に切って,切る前の基の長さは,半分のテープの2つ分であり,これは2倍とも言うとある。つまり,倍は「いくつ分」から説明されている。
東京書籍は,かけ算の最初の章で,「2この3つぶんを,2この3ばいといいます」(2下 1970 p.63)と書かれていて,やはり,倍がいくつ分から説明されている。
しかし,いくつ分と倍は完全に同じではないであろう。上記オレンジ色の画像に「うまは、かめの何倍ですか」とはあるが、ウマの数とカメの数という2つの量の大きさの関係を、カメの数を基準として、問うている。ここでは、倍は比である。かめの数2の3倍が,うまの数6なのである。
かけ算はもはや,たし算の特殊な場合の簡略表記ではない。あくまで、2つの量の大きさの関係なのである。しかも,それは単なる静態的な関係(比)ではなく、「倍加する」という運動,働きでもある。かめは2匹であり、うまの数6匹は、それを3倍に「引き伸ばした」大きさなのである。
注意すべきは,ここでは、カメはウマの一部(単位)ではない、ということである。これは,〈1つ分×いくつ分〉による定義と違う点である。1つ分は基本的に全部の量の物理的な一部である。また,いくつ分が量であるのに対して,倍が量ではなく関係・働きである点でも,違っている。
被乗数×乗数にしても,一つ分×いくつ分にしても,乗号の前後は非対称的であるが,基準量×倍は,この非対称性が際立っている。倍を表す数は,事物が直接表す量ではなく,量と量との関係であり,その点でより抽象的である。
この時代には、かけ算の式の〈言葉の式〉(公式)は,東京書籍では,とくに,これに対応する公式はないようだが,学校図書では,
もとの数×かける数=答え
となっている。さらに,倍という概念をここに含ませれば,
もとの数(量)×何倍=全部の数(量)
となるであろう。
「かけられる数」(被乗数)と「かける数」(乗数)は,同数累加でかけ算が定義されていた時代の概念である。東京書籍では,それらは定義されていないが,言葉としては九九表に使われている。学校図書では,九九表の「かけられる数」のところが「もとの数」になっている。
かけ算が倍で定義される時代になって,同数累加が否定されたかというと,そうではなく,「4×3のこたえはつぎのけいさんでだすことができます。4+4+4=12」(東京書籍 p.65)と,書かれている。
つまり,同数累加は,もはや掛け算の定義ではないが,かけ算をたし算でも表せるという付随的な指摘のなかで生きている。これは,現在の教科書もそうなっている。また,学校図書では「3+3+3+3は3の□倍です。」といった問題があり,倍は被乗数・乗数の乗数に対応するものであることがわかる。
このように,かけ算は倍をメインに定義されているが,同数累加や〈1つ分×いくつ分〉が消滅したわけではなく,周縁に退いただけである。倍の時代に,倍がいくつ分から説明されていることを考えれば,根底的には,かけ算は本源的には「いくつ分」なのであろう。
3.1980年代~2020年代
現代化の時代が終わると、かけ算の定義は、〈基準量×倍〉から、〈1つ分×いくつ分〉へと変わった。
倍による定義は、小学校の低学年生には少々、高度であった。というのも、倍は量と量の関係を表す数(比)だから。
現代化時代に、日本の算数教育は、現代数学の概念を取り入れていたずらに形式化・高度化に走り、大量の数学嫌いを作ってしまった。このことに対する反省から、日本の算数教育は、基礎と具体性へと帰ることになった。
その際、教科書が取り入れたのが、数教協の〈一あたり量×いくつ分〉というかけ算定義であった。同数累加の簡略算という定義では、乗数が小数や分数のかけ算ががうまく説明できなかった。そのため、数教協は乗数を量化したのである。
数教協の概念は、一般には、かけわり図や組立単位など、小学生には難しいものばかりであるが、教科書に取り入れられた次のかけ算図式は、低学年でも十分に理解しやすいものてあった。
①〈1つ分の数×いくつ分=全部の数〉
②〈1つ分の大きさ×いくつ分=全部の大きさ〉
①は②の分離量バージョンである。これは、英語圏では、同数グループによる定義と、親和性が高い。英語圏では、かけ算は、3×4というかけ算の式は、しばしば、3 groups of 4という自然言語表現に基づいて学ばれる。
〈1つ分×いくつ分〉によって、乗数は、7を4回足すというときの回数ではなく、具体的な量となった。だから、ピザ1枚900gで、2枚半(2.5)では何gのようなことが考えられるようになった。乗数はここでは、倍のような関係でもなく、分量を表している。
倍による定義では、比較される2つの量は、種類は同じくするかも知れないが、別の物体であった。〈1つ分×いくつ分〉では、一つ分はいくつ分の一部をなしている。ピザ1枚は2枚半の一部を構成している。乗数は具体的な量なので、絵に描くことができる具体性をもつ。
このように、1980年代に、日本の算数教育では、かけ算は〈1つ分×いくつ分=全部の数〉で定義されるようになった。だが、他の時代もそうであったが、メインの定義が替わっただけで、他の定義が消滅したわではなく、ただ周縁化しただけである。
事実、定義の少しあとでは「3×3は3+3+3で求められます」と言われている。同数累加による定義は、定義の一部ではなくなったが、このように、かけ算の言い換え表現として生き残っている。
また、「2の8つ分は2の8倍とも言う」と言われており、倍による定義も生きている。倍の時代に、倍はいくつ分で導入され、いくつ分の時代に、いくつ分は倍で言い換えられる。
だが、このようにほぼ同時に導入される〈基準量×倍〉は、高学年になると、〈基準量×割合〉へと発展して行くものであるが、〈1つ分×いくつ分〉から〈基準量×倍〉へ、〈基準量×割合〉への移行には、小学校の先生方も苦労しているようである。
注
注1
第7巻「定義16 数に数を掛けるといわれるのは、後者の中にある単位の数と同じ回数だけ前者、すなわち【掛けられる数】が加え合わされてなんらかの数が生ずるときである。」(『ギリシアの科学』 p.331)
(Twitterに2020/02/21, 03/01, 05/30に投稿された、flute23432のツイートに基づく。)